시련은 있어도, 실패란 없다
- 정주영 ( 현대 그룹 창업자 )
지금까지 우리는 모델을 훈련할 때, 표준적인 경사하강법(Gradient Descent Algorithm)만 써왔습니다. 하지만 이러한 훈련과정의 속도를 높이는 방법에 대해 초기화 / activation function / Batch-Normalization / 전이 학습 4가지를 공부했습니다.
이번 포스팅에서 공부할 것은 훈련 속도를 높이기 위해 경사 하강법 대신에 쓸 수 잇는 고속 옵티마이저에 대해서 공부해보겠습니다.
다음 포스팅을 먼저 정독하시고 이번 포스팅을 보시면 더욱 쉽게 이해하실 수 있습니다 :)
[AI/Hands-On Machine Learning 2판] - [머신러닝 순한맛] 그레디언트 소실(Vanishing) / 폭주(Exploding)이란?
[머신러닝 순한맛] 그레디언트 소실(Vanishing) / 폭주(Exploding)이란?
잘못된 전략이라도 제대로 실행만 하면 반드시 성공할 수 있다. 반대로 뛰어난 전략이라도 제대로 실행하지 못하면 반드시 실패한다. - 선 마이크로시스템즈 CEO, 스콧 맥닐리 - Deep Neural Network,
box-world.tistory.com
모멘텀 최적화(Momentum Optimization)
우리가 기존에 배웠던 경사 하강법은 경사면을 따라 일정한 크기의 스텝으로 조금씩 내려갑니다. 반대로 모멘텀 최적화는 경사를 굴러가는 볼링공과 같습니다. 즉 처음에는 느리게 출발하지만, 시간이 지날수록 빠르게 가속되어 결과적으로 더 빠릅니다.
경사 하강법은 다음과 같이 loss 그레디언트 * 학습률을 기존 가중치에 뺌으로써 갱신이 이뤄집니다. 이러한 방식이 이전 그레디언트가 얼마였는지 고려하지 않습니다. 그렇기 때문에 부분적으로 그레디언트가 작으면 매우 느려집니다.
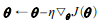
모멘텀 최적화는 경사 하강법과 반대로 이전 그레디언트가 얼마였는지가 중요합니다. 여기서는 매 반복에서 그레디언트 * 학습률를 구하여 이를 모멘텀 벡터 $m$에 더한 값을 빼서 가중치를 갱신하게 됩니다. 쉽게 생각해서 이 모멘텀 벡터에 이전 그레디언트에 대한 정보가 담겨있다고 생각하면 됩니다.
그런데 여기서 볼링공이 너무 빠르게 내려가지 않도록 일종의 마찰 저항을 주기 위해 새로운 하이퍼 파라미터 $β$가 등장합니다. 이 값이 커질수록 마찰 저항이 없어지는데 보통은 $0.9$로 설정합니다. 이렇게 설정하면 경사 하강법보다 10배 정도 빠르게 최적화를 진행할 수 있습니다.

어떤 입력 데이터의 스케일이 다르면, 비용 함수는 길쭉한 타원형의 모양을 가지게 됩니다. 경사 하강법은 이러한 경우에 매우 느립니다. 그러나 모멘텀 최적화는 굉장히 빠르게 minimum loss에 도달할 수 있습니다.
이러한 모멘텀 최적화는 Batch-Normalization을 사용하지 않아서 스케일이 다른 입력이 들어오는 Neural Network에 적용하면 좋습니다. 다음은 Keras에서 모멘텀 최적화를 구현하는 코드입니다.
optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9)
네스테로프 가속 경사
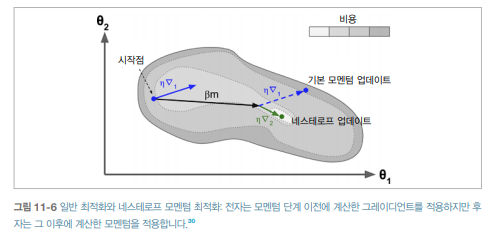
NAG라 부르는 네스테로프 가속 경사는 모멘텀 최적화의 변종으로 기존보다 거의 항상 빠릅니다. 기존에는 현재 위치에서 그레디언트를 계산했었다면, 모멘텀의 방향으로 즉 볼링공이 흘러가는 방향으로 조금 앞선 위치에서 그레디언트를 계산합니다.

아래 그래프를 보면 알 수 있듯이 NAG가 minimum loss에 좀더 가깝습니다. 이러한 작은 개선이 쌓여서 NAG가 기존 모멘텀 회적화보다 확연히 빨라지게 됩니다. 게다가 기존 모멘텀 업데이트는 방향이 정해져 있기 때문에 의도와 달리 minimum loss쪽으로 가중치가 흘러가지 않을 수 있습니다. 그러나 NAG의 경우는 minimum loss쪽으로 가중치를 끌어당겨 진동을 감소시키고 수렴을 빠르게 합니다.
다음은 NAG를 Keras에서 사용한 코드입니다.
optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9, nesterov=True)
AdaGrad
방금 우리가 NAG와 경사 하강법의 최적화를 비교했던 바로 위 그래프를 다시 보겠습니다. 경사하강법은 가장 가파른 경사를 빠르게 내려가기 시작하여 골짜기 아래로 느리게 이동합니다. 만약 알고리즘이 이를 빠르게 감지하여 global minimum 쪽으로 정확한 방향을 잡아줬다면 좋았을 것입니다. 이를 위해 그레디언트 벡터의 스케일을 감소시켜 해결하고자 하는게 AdaGrad 알고리즘입니다.

첫번째 단계는 그레디언트의 제곱을 벡터 x에 누적합니다. 만약 비용함수가 i번째 차원을 따라 가파르다면, 기울기가 클 것이므로 $s_i$또한 반복이 진행됨에 따라 점점 커지게 됩니다.
두번째 단계는 경사 하강법과 거의 같습니다. 다만 한 가지 차이는 그레디언트 벡터를 루트값으로 나누어 스케일을 조정합니다.
AdaGrad는 학습률을 감소시키지만, 경사가 완만한 차원보다 가파른 차원에 대해 더 빠르게 감소됩니다. 이를 적응적 학습률이라 부르며 global minimum 방향으로 곧장 가도록 갱신하는데 도움을 줍니다.
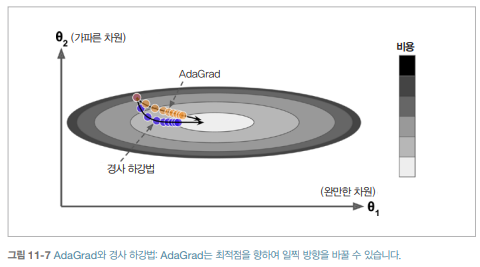
AdaGrad는 간단한 2차 방정식 문제에 대해서는 잘 작동하지만, 학습률이 너무 감소되어서 global minimum이 도착하기 전 알고리즘이 멈추는 경우도 있습니다. 따라서 간단한 작업에서만 사용하고, Neural Network같이 복잡한 작업에서는 사용하지 않는 것이 좋습니다.
RMSProp
AdaGrad이 global minimum에 잘 도달할 수 있는 이유는 빠르게 내려가는 학습률이 방향 전환을 쉽게 해주기 때문입니다. 그러나 너무 빨리 느려져 global minimum에 도달하지 못할 수 있다는 위험도 내재되어있습니다.
RMSProp은 전체가 아닌 최근 반복에서 비롯된 그레디언트만 누적하여 이 문제를 해결했습니다. 이를 위해 알고리즘의 첫번째 단계로 지수 감소(Exponential Decay)를 사용합니다.

보통 감쇠율 $β$는 0.9로 설정합니다. 다음은 Keras로 구현한 코드입니다.
optimizer = keras.optimizers.RMSprop(lr=0.001, rho=0.9)Adma과 Nadam
adaptive moment estimation의 줄임말인 Adam은 모멘텀 최적화와 RMSProp의 아이디어를 합친 것입니다. 모멘텀 최적화처럼 지난 그레디언트의 지수 감소 평균을 따르고, RMSProp처럼 지난 그레디언트 제곱의 지수 감소 평균을 따릅니다.

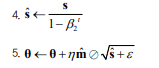
단계 1,2,5를 보면 Adam이 모멘텀 최적화, RMSProp과 아주 비슷하다는 것을 알 수 있습니다. 차이점은 단계 1에서 지수 감소 합 대신 지수 감소 평균을 계산하는 것이지만, 사실 상수 배인 것을 제외하면 동일합니다.
$m$,$s$는 초기화로 인해 훈련 초기에 0쪽으로 치우치게 될 것입니다. 그래서 이 두 단계가 훈련 초기에 $m$과$s$를 증폭시키는데 도움을 줄 것입니다.
다음은 Keras에서 적용한 코드입니다.
optimizer = keras.optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.999)Adam 또한 적응적 학습률 알고리즘이기 때문에, 학습률 하이퍼파라미터를 튜닝해주지 않아도 됩니다.
이제 지금껏 나온 옵티마이저를 비교해보겠습니다.

다음 포스팅에서는 학습률 스케줄링에 대해 공부해보겠습니다. 오늘도 함께해주셔서 감사합니다. 행복한 하루 보내세요 :)