"경쟁자의 성공을 탐하지 마라"
- 제럴딘 레이본느 (옥시전 미디어 회장 겸 ceo) -
저번 포스팅에서 우리는 가중치 파라미터의 최적화를 속도, 그리고 리소스 효율성의 측면에서 바라보았습니다. 이번 포스팅에서는 최적화의 속도에 관여하는 또 하나의 하이퍼파라미터인 학습률(Learning Rate) 스케줄링을 통해 파라미터 최적화의 성능을 방법에 대해서 알아보겠습니다.
학습률 스케줄링
가중치를 최적화하는데 있어서 '좋은 학습률'을 찾는 것은 중요한데 이유는 다음과 같습니다. 우리가 가장 Loss가 적은 Local minimum까지 걸어간다고 할때, 학습률은 걸음의 보폭이라고 할 수 있습니다. 학습률이 너무 크면 Local minimum을 지나치거나 수렴하기 어렵습니다. 반대로 너무 작아도 Local minimum까지 도달할 순 있어도 그 시간이 매우 오래 걸릴 것입니다.

이제 학습률의 중요성을 알았으니 본격적으로 다양한 학습률 스케줄링 방식에 대해 하나하나 살펴보겠습니다.
1) 거듭제곱 기반 스케줄링(Power Scheduling)


- $t$ : Training epoch(반복 횟수)
- $n_0$ : 초기 학습률
- $c$ : 상수
- $s$ : 스텝 횟수 (우리가 지정해야하는 하이퍼 파라미터로써 스텝은 우리가 지정한 데이터의 크기만큼을 한번 훑으면 1번의 스텝으로 여기므로 전체 데이터셋을 한번 훑었을때 1번으로 여기는 epoch와는 다른 개념입니다.)
위 수식을 쉽게 해석해보면 $s$, $c$, $n_0$은 고정된 값이고, $t$는 학습이 진행될 수록 늘어나는 값이다. 그런데 이 늘어나는 $t$가 늘어날수록 분모가 늘어나면서 $n(t)$는 감소하게 됩니다. 즉 학습이 진행될수록 학습률은 감소하게됩니다.
처음엔 Local Minimum이 멀리있을테니 긴 보폭으로 다가가다가 거의 다왔을때는 보폭을 줄여 Local minimum에게 세심하게 가까이 가려는 건 당연한 순리겠죠.
다만 초기 학습률 $n_0$과 $s$는 우리가 지정해줘야하는 하이퍼 파라미터에 속합니다.
2) 지수 기반 스케줄링 (Exponential Scheduling)
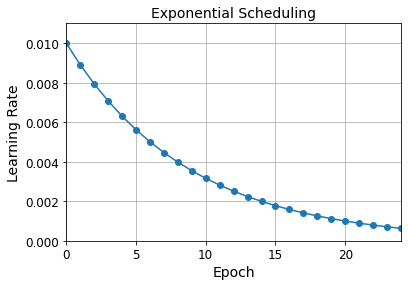

- $t$ : Training epoch(반복 횟수)
- $s$ : 스텝 횟수
$t=s$일땐 $(0.1)^1$, $t=2s$일땐 $(0.1)^2$ 이런 식으로 t가 늘어날 때마다 학습률이 감소되는 스케줄링 방식입니다. 다만 1)과 달리 s번의 스텝마다 고정적으로 10배씩 감소한다는 점에서 차이를 두고 있습니다.
3) 구간별 고정 스케줄링 (Piecewise Constant Scheduling)

일정 횟수의 에포크 동안 일정한 학습률을 사용하고, 그 다음 또 다른 횟수의 에포크 동안은 더 작은 학습률을 사용하는 식입니다. 예를 들어 초기 5 에포크 동안에 $n_0= 0.1$, 그 다음 50에포크 동안에 $n_0=0.001$ 이런식으로 우리가 직접 지정하여 스케줄링하는 방식입니다. 다만 성능을 높이기 위한 최적의 조합은 우리가 직접 찾아야합니다.
4) 성능 기반 스케줄링 (Perfomance Scheduling)

매 $N$번의 스텝마다 Validation Loss를 측정하고, 이것이 줄어들지 않으면 $i$배만큼 학습률을 감소시킵니다.
5) 1 사이클 스케줄링 (1cycle Scheduling)
이 방식은 다른 방식과 조금 다른 방식을 지닙니다. 1 사이클은 훈련 절반 동안 초기에 지정한 학습률 $n_0$을 선형적으로 $n_1$까지 증가시킵니다. 그 다음 나머지 절반 동안은 증가되었던 $n_1$을 $n_0$으로 선형적으로 되돌립니다. 그리고 마지막 몇 번의 에포크 동안의 학습률은 소수점 몇 째자리까지 선형적으로 줄입니다.
최대 학습률 $n_1$은 우리가 직접 지정해야하며, 초기 학습률 $n_0$은 보통 10배 정도 낮은 값을 선택합니다. 모멘텀 사용시(모멘텀은 마찰을 의미합니다. 모멘텀이 높을 수록 마찰이 심해질수록, 높은 학습률을 가지더라도 앞으로 멀리가기 힘들어진다고 이해하면 됩니다.), 처음에는 높은 모멘텀으로 시작하여 학습률을 제어시켰다가 최대 학습률에 되는 절반 지점까지 점점 모멘텀을 줄입니다. 그리고 나머지 절반동안 학습률이 다시 초기 학습률 $n_0$로 돌아가는 동안 점진적으로 모멘텀을 높입니다.
이 방식은 여러 연구를 통해 충분히 검증된 훌륭한 방식입니다.
2013년도 논문에 따르면 모멘텀 최적화를 사용한 음성 인식용 Neural Network를 훈련할 때 가장 널리 알려진 학습률 스케줄링의 성능을 비교했습니다. 저자들은 성능 기반 스케줄링과 지수 기반 스케줄링이 둘다 잘 작동했지만, 튜닝이 쉽고 Local minimum에 조금 더 빨리 수렴하는 지수 기반 스케줄링이 선호된다고 결론을 내었습니다.
다음은 거듭제곱 기반 스케줄링을 keras에서 구현한 것입니다. 여기서 decay는 우리가 앞서 보았던 스텝 수 $s$의 역수입니다. (keras는 이를 1로 가정합니다.)
optimizer = keras.optimizers.SGD(lr=0.01, decay=le-4)다음은 지수 기반 스케줄링입니다.
def exponential_decay_fn(epoch):
return 0.01 * 0.1**(epoch / 20)하지만 위와 같이 하면 $n_0$와 $s$가 바뀔때마다 새로 함수를 정의해야하므로, 이 둘을 매개변수로 추가하여 LearningRateScheduler 콜백을 만들어보겠습니다.
def exponential_decay(lr0, s):
def exponential_decay_fn(epoch):
return lr0 * 0.1 ** (epoch / s)
return exponential_decay_fn
exponential_decay_fn = exponential_decay(lr0=0.01, s=20)
lr_scheduler = keras.callbacks.LearningRateScheduler(exponential_decay_fn)
history = model.fit(X_train_scaled, y_train, [...], callbacks=[lr_scheduler])구간별 고정 스케줄링 방식도 별도의 함수를 LearningRateScheduler 콜백을 만들어 fit() 메서드에 전달합니다. 다음은 다섯 번의 에포크 동안 향상되지 않을때마다 학습률에 0.5를 곱합니다.
def piecewise_constant_fn(epoch):
if epoch < 5:
return 0.01
elif epoch < 15:
return 0.005
else:
return 0.001
lr_scheduler = keras.callbacks.LearningRateScheduler(piecewise_constant_fn)마지막으로 tf.keras에서는 keras.optimizers.schedules에 있는 스케줄 중에 하나를 사용해 학습률을 정의하고 이것을 옵티마이저에 전달하는데 이렇게 하면 에포크가 아니라 매 스텝마다 학습률을 업데이트합니다. 다음은 이를 이용해 지수 기반 스케줄링을 구현하는 방법입니다.
s = 20 * len(X_train) // 32 # number of steps in 20 epochs (batch size = 32)
learning_rate = keras.optimizers.schedules.ExponentialDecay(0.01, s, 0.1)
optimizer = keras.optimizers.SGD(learning_rate)
다음 포스팅에서는 Regularization을 이용해 Overfitting을 피하는 방법에 대해 알아보겠습니다. 오늘도 읽어주셔서 감사합니다. 행복한 하루 보내세요 :)
'AI > Hands-On Machine Learning 2판' 카테고리의 다른 글
| [ 머신러닝 순한 맛 ] 시계열 데이터의 모든 것, RNN 정복하기! (2) | 2021.07.28 |
|---|---|
| [ 머신러닝 순한맛 ] Regularization in 딥러닝의 모든 것 (2) | 2021.07.05 |
| [ 머신러닝 순한 맛] 전이학습은 어떻게 이뤄질까? with Code (1) | 2021.05.11 |
| [머신러닝 순한맛] 그레디언트 소실(Vanishing) / 폭주(Exploding)이란? (1) | 2021.05.02 |
| [ 핸즈 온 머신러닝 2 ] 비지도 학습의 모든 것 (K-Means) (1) | 2021.02.08 |