시작하며
이번 포스팅에선 정확하고 효율적인 머신러닝을 위해서, 데이터의 Feature가 어떤 영향을 끼치는지 알아보겠습니다.
겹치는 Feature는 합치자

위는 제가 참여했던 대회에서 버스 정보를 이용하여 버스의 도착 시간을 예상하는 모델 을 만들어 보라고 저에게 주어진 데이터입니다.
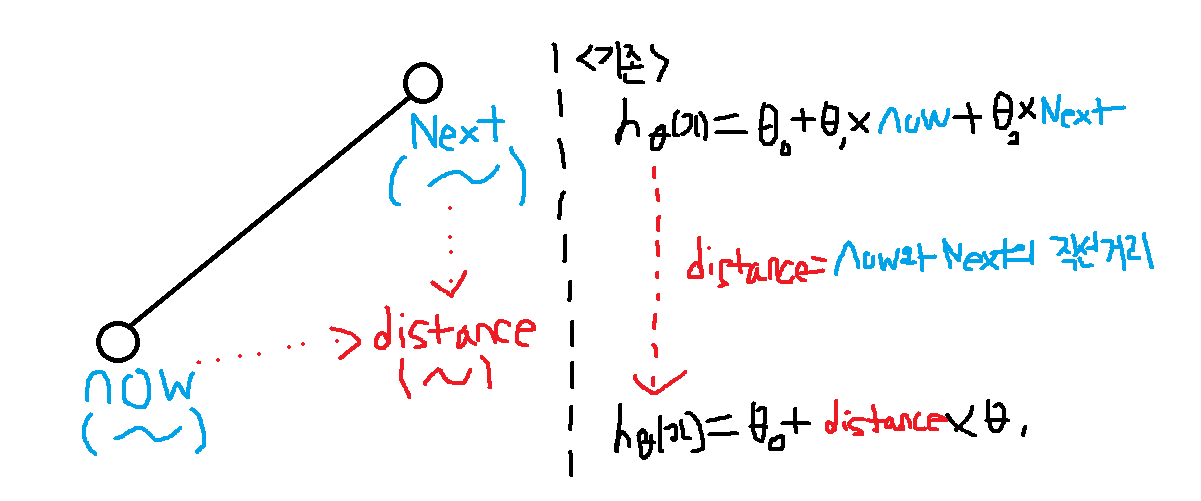
주어진 데이터의 feature에는 1)출발 지점의 위도(now) 와 2)도착 지점의 위도(next) 가 포함되어있었습니다.
이 둘을 그대로 학습에 적용할 수도 있지만 이 두 feature 대신 두 위도의 직선거리라는 새로운 feature로 대체 하여 전체 feature의 갯수를 줄인다면, 가설함수 h는 훨씬 심플 해지지 않을까요?
이처럼 모델 학습에 앞서 feature를 합치거나 필요가 없는 feature는 과감히 삭제해버리는 과정 을 통해 학습의 정확성과 효율성을 높일 수 있습니다.
이러한 결과는 많은 분들께서 학습 모델 결정만큼이나 학습할 데이터의 가공 을 강조하는 이유입니다.
다항 회귀(Polinomial regression)

위는 집의 크기(Size)로 가격(Price)을 예측하고자 하는데, feature가 2개여서 가설함수 h가 이차방정식 인 상황입니다.
결론적으로 이차방정식인 가설함수 h는 여기에 적절하지 않습니다.
왜냐하면 우리의 상식에선 집의 Size가 커질수록 Price도 비례 하여 커져야합니다.
하지만 이차방정식은 대칭축을 기점으로 꺾이게 되고 이는 우리의 상식과 모순 됩니다.
이때 사용할 수 있는 것이 다항 회귀(Polinomial regression) 입니다.

우리에게 문제가 되었던 이차방정식의 가설함수가 만약 삼차방정식이 된다면, 변곡점에서 증가가 둔화되긴 하지만 쭉 증가한다는 것은 분명합니다.
이렇게 2차식에서 3차식으로 변환하기 위해선 x1~x3를 (size)^1부터 (size)^3으로 치환해주면 됩니다.
다만 이렇게 하면 (size)^1부터 (size)^3의 범위(range)가 이미지상의 파란글씨처럼 모두 달라지기 때문에 range를 맞춰주기 위한 feature scaling이 매우 중요해집니다.
이렇듯 Polynomial regression은 Input과 Output의 관계가 비선형적일 경우 이를 선형 회귀(linear regression)으로 확장하는 표준적인 방법 입니다.
요약
1) 데이터를 분석하고 필요에 따라 feature를 합치거나 제거하면 경우에 따라 학습의 정확성과 효율성을 높일 수 있다.
2) Polynomial regression은 Input과 Output의 관계가 비선형적일 경우 이를 선형 회귀(linear regression)으로 확장하는 표준적인 방법이다.
3) Polynomial regression을 사용할 땐 feature scaling이 중요하다.
'AI > Coursera ( Machine Learning )' 카테고리의 다른 글
| [머신러닝] Logistic Regression 이해하기 2 (2) | 2020.04.30 |
|---|---|
| [머신러닝] Logistic Regression 이해하기 1 (1) | 2020.04.30 |
| [머신러닝] Normal Equation vs Gradient Descent Algorithm(경사 하강 알고리즘) in 선형 회귀(linear regression) (0) | 2020.04.30 |
| [머신러닝] 데이터 전처리(Feature Scaling)을 이용한 경사 하강 알고리즘(Gradient Descent Algorithm) (1) | 2020.04.30 |
| [머신러닝] 다변수 선형 회귀(Multivariable Linear Regression )이란 (1) | 2020.04.30 |