시작하며
우리는 그동안 Supervised Learning 에서 회귀(Regression) 를 중점적으로 다뤘습니다. 이때 회귀 란 결과값을 예측하는 것이었습니다.
이제부터는 마찬가지로 Supervised Learning 중 하나인 분류(Classification) 을 배워보겠습니다.
Classification

Classification 이란 어떤 기준에 의해 데이터를 처리하고 이를 A인지 B인지 내지는 1인지 0인지 식의 결과값 을 얻고 싶을 때 사용합니다.
앞으로 우리는 이렇게 이분법적으로 분류하는 Binary Classification 을 공부할 것이며 2가지 이상으로 분류하는 Multiple Classification 도 앞으로 차차 공부하게 될것입니다.
EX)
- 이메일이 Spam vs Not Spam
- 온라인 거래가 Froud(사기) vs Non-Froud
- 종양을 관측하고 Cancer(암) vs Non-cancer
일반적으로 True / False를 가릴 때,True =1 / False = 0 으로 표현하고 이를 각각 Positive class / Negative class라고 합니다. 예를 들어 이메일 분석 결과가 1이면 Spam 0이면 Not Spam인 것입니다.
이번 포스팅은 Linear regression을 이해하고 보시면 훨씬 효과적입니다.
https://box-world.tistory.com/6?category=397062
Linear Regression to Classification?
우선 우리가 잘 아는 Linear Regression을 Classification에 이용해보겠습니다.
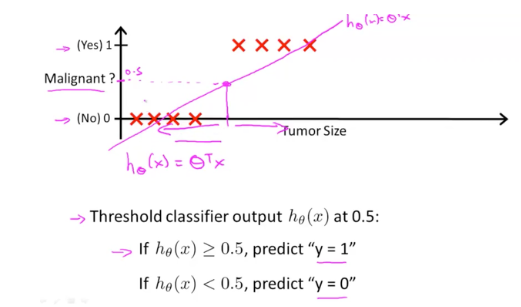
위 샘플 데이터는 종양 사이즈(Tumor Size)가 일정 수준 이상으로 넘어가면 악성 종양이라고 판단하는 dataset 입니다.
우리는 들어온 데이터가 악성인지(true / 1) 아닌지(false / 0) 판단하기 위해 Linear Regression을 적용한다면 위와 같이 핑크색 선 을 그어볼 수 있을 것입니다.
위의 경우에 종양 사이즈가 0.5를 기준삼아 이 이상이면 악성이다(true / 1)라고 판단하고 그 이하일 땐 아니다(false / 0)이라고 판단하겠습니다.
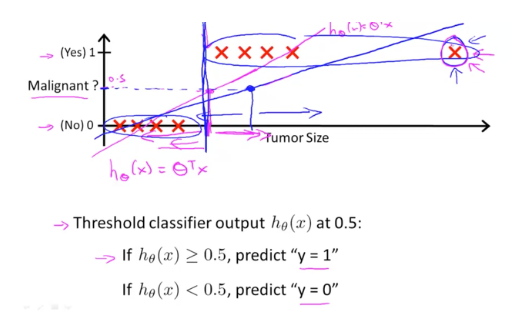
만약 여기에 사이즈가 엄청나게 큰 종양(Tumor Size가 매우 큰)이 데이터에 들어왔다고 해보겠습니다. 이때 Linear Regression을 Classification에 적용했을 때 문제점이 나타납니다.
사이즈가 엄청 큰 종양이 들어왔다는 것은 결국 데이터의 범위(range)가 넓어졌다는 것이고, Linear Regression에서 가설함수란 데이터를 대표하는 함수입니다. 따라서 가설함수인 직선은 데이터를 반영하여 파란색 선처럼 기울어지게 됩니다. 따라서 우리가 기존에 약성 종양을 판단하던 기준점이 0.5가 아닌 그 이상의 큰 값이 됩니다.
구체적인 예로 만약 기준점이 0.7로 이동했다면, 기존에는 0.55, 0.61등이 악성 종양으로 판단되어야 했지만 이는 0.7 미만이기 때문에 저 경우엔 정상으로 판단이 되고 이는 매우 큰 문제입니다.
결론은 Linear Regression은 Classification에 적용할 수 없습니다.
Logistic Regression

또 다른 문제는 우리가 원하는 결과값은 0 혹은 1인데 Linear Regression에서 사용하는 h(x)에선 1보다 크거나 0보다 작은 값이 나올 수 있다는 것입니다.
그래서 우리가 사용할 h(x)가 0과 1사이의 값을 가지도록 해결하기 위해 나온 것이 Logistic Regression입니다.
따라서 앞으로 Classification을 할 땐 Logistic Regression을 적용한다고 생각하시면 됩니다.
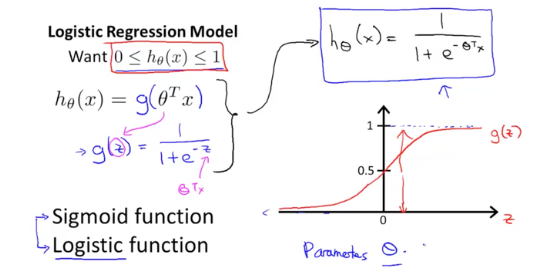
우리가 Classification에서 h(x)의 결과값이 0과 1사이로 나오길 원하는 이유 는 0과 1사이 어떤 기준점을 세우고 1에 가까우면 true, 0에 가까우면 false 이런 식으로 판단하기 위해서 입니다.
이를 위해 우리가 기존에 Linear Regression에서 사용하던 h(x)(θ^Tx)를 함수 g에 대입해줍니다. 이 g 함수는 Logistic 혹은 Sigmoid 함수 라고 부릅니다. 위 함수 그래프가 g 함수인데 보다시피 0과 1사이의 함수값을 가지며 0.5를 통과하는 s자 모양의 함수입니다. 이렇게 해서 나온 g(θ^Tx)가 Classification에서 사용할 가설함수가 됩니다.

그렇다면 Logistic Regression에서 사용하는 h(x)(=g(θ^Tx))의 함수 값은 어떤 의미일까요?
이는 곧 가능성(probability)를 의미하며 특정 x에서 y가 1일 가능성이 얼마인지를 알려주는 것입니다. 가령, h(x)가 0.7이라면 결과가 1일 가능성이 70%인 것입니다.
이러한 h(x)를 P로 나타낼 수 있습니다. 위 이미지에서 아랫 부분을 요약하자면, y = 1일 가능성을 x와 θ로 나타낼 수 있습니다. 또한 y = 0일 가능성은 '1 - (y가 1일 가능성' 입니다.
Decision Boundary

Decision Boundary란 말 그대로 결과값 y를 0으로 판단할지 1로 판단할지 나누는 기준선입니다.
위처럼 우리가 어떤 값을 분류함에 있어서 3개의 feature가 이용되어 θ0 + θ1x1 + θ2x2를 g에 대입하여 h(x)를 설정하였습니다.
Logistic Regression에서는 주어진 데이터를 최대한 잘 분류할 Decision Boundary의 각각의 θ값을 찾아내는 것이 목표이며 위 이미지는 θ를 임의로 -3, 1, 1로 설정했을 때 나타나는 Decison Boundary입니다.
따라서 위 경우에서 임의로 설정할 θ를 넣었을 때 나타나는 저 핑크색 선 위로 데이터가 분포하면 y = 1이라고 판단하게 되는 것입니다.

기준을 나누는 h(x)가 꼭 직선인 것은 아닙니다. 위 경우 h(x)를 이차방정식 θ0 + θ1x1 + θ2x2 + θ3x1^2 + θ4x2^2이라고 하고 θ도 아까와 같이 임의로 설정하였습니다.
그때 h(x)는 원의 방정식으로 직선이 아닌 원의 형태 를 띄게 되며 원의 바깥쪽은 1, 안쪽은 0이라고 판단하게 됩니다.
이외에도 h(x)는 다양하고 불규칙한 모양일 때 3차, 4차 다항식으로도 나타나집니다. 결론은 Decision Boundary의 형태는 매우 다양합니다. 그리고 이를 결정하는 θ를 어떻게 찾아 h(x) 만드는지 다음 포스팅에서 알아보겠습니다.
요약
1) Classification 이란 데이터를 1 또는 0으로 분류하는 것이다.
2) Classification에는 Logistic Regression이 적용된다.
3) Logistic Regression에서의 h(x) 함수값은 가능성(probability)를 의미하며 특정 x에서 y가 1일 가능성이 얼마인지를 알려주는 것이다
4) Decision Boundary란 말 그대로 y가 0인지 1인지를 판단하는 기준선이며 형태는 매우 다양하게 나타날 수 있다.
[머신러닝] Logistic Regression 이해하기 2
'AI > Coursera ( Machine Learning )' 카테고리의 다른 글
| [머신러닝] 여러 개로 분류하기(Multi Classification) (1) | 2020.04.30 |
|---|---|
| [머신러닝] Logistic Regression 이해하기 2 (2) | 2020.04.30 |
| [머신러닝] Feature 선택과 다항 회귀(Polinomial regression) (0) | 2020.04.30 |
| [머신러닝] Normal Equation vs Gradient Descent Algorithm(경사 하강 알고리즘) in 선형 회귀(linear regression) (0) | 2020.04.30 |
| [머신러닝] 데이터 전처리(Feature Scaling)을 이용한 경사 하강 알고리즘(Gradient Descent Algorithm) (1) | 2020.04.30 |