시작하며
저번 포스팅 'Back Propagation' 이라는 Neural Network의 큰 고비를 넘기신걸 축하드립니다.
오늘은 지금까지 배운 Neural Network 개념을 토대로 어떻게 Network를 설계해야 하는가에 대해 공부해보겠습니다.
Neural Network에 대한 개념이 부족하신 분은 아래 포스팅부터 봐주시면 되겠습니다.
- [쉬운 머신러닝] 딥러닝의 시작 Neural Network 정복하기 1
https://box-world.tistory.com/17
Neural Network의 구성

Neural Network의 구성요소는 크게 Input Layer, Output Layer, Hidden Layer로 나뉩니다.
Input units
Input Layer를 구성할 때 Unit의 갯수는 학습할 dataset의 features의 갯수 가 됩니다.
Output units
Output Layer를 구성할 때 Unit의 갯수는 Classification 해야하는 class의 수 와 같습니다.
Hidden units
Hidden Layer를 구성할 때 Unit의 갯수는 보통 Input Unit 갯수의 배수 로 정하게 되지만, 공식이나 정답은 정해져있지 않습니다. 다만 하나의 Network안에서 Hidden Layer가 여러개라면 모든 hidden Layer의 unit 갯수는 동일해야 합니다.
하지만 역시 마찬가지로 하나의 Network안에서 Hidden Layer가 몇개여야 하는지 알 수 있는 정답이나 공식은 존재하지 않습니다.
다만 많아지면 많아질 수록 좋은 결과는 보여주겠지만 연산이 복잡해지므로 학습시간이 오래 걸릴 것입니다. 결국 Neural Network를 설계할 때 Layer의 갯수나 Unit의 수를 어떻게 설정한것인지 가 중요한 요소 중 하나가 됩니다.
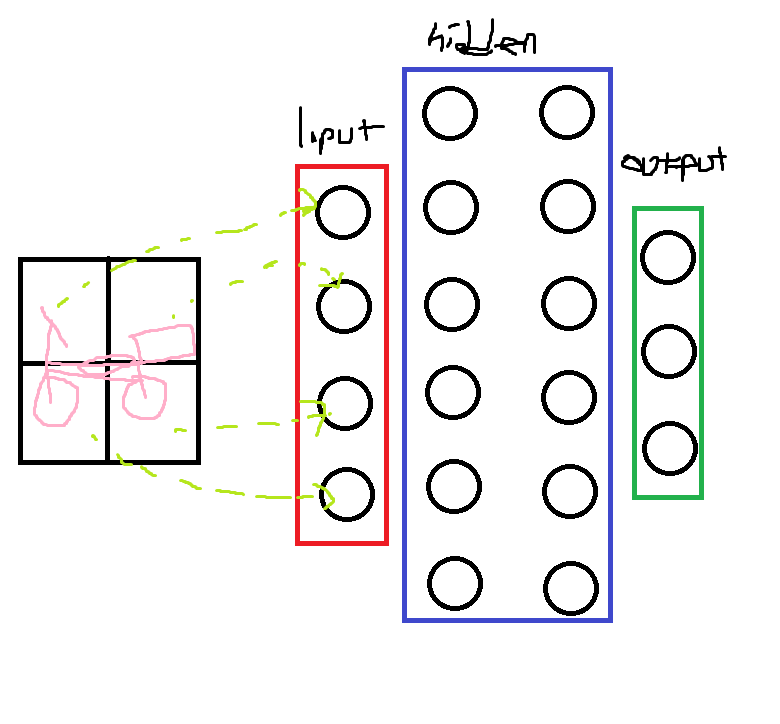
예를 들어, 입력된 이미지를 보고 자동차, 자전거, 트럭 중 하나로 분류하는 경우를 생각해보겠습니다.
우선 Input data는 이미지의 '픽셀'이 됩니다. 이 경우 2x2 즉 4개의 feature라고 가정해보겠습니다. 따라서 Input Layer의 unit 수는 4개가 됩니다.
Output Layer에선 이미지를 자동차, 자전거, 트럭 즉 3개의 class 중 하나로 예측할 것이므로 Unit의 갯수는 3개가 되어야 합니다.
Hidden Layer는 정해진건 없지만 2개라고 하고, 각 Layer의 Unit 갯수는 Input Unit의 1.5배인 6개라고 설정해볼 수 있습니다.
Neural Network의 구현
이제 Neural Network를 어떻게 구현하는지 6단계로 나눠 알아보며 구현 과정에서 주목해야할 이슈에 대해 알아보겠습니다.
1. Weight값 설정
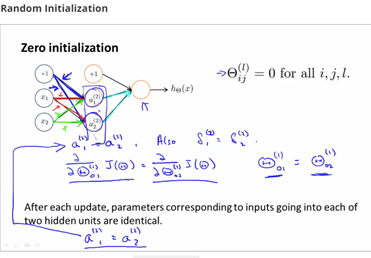
맨 처음 가중치값 θ를 전부 0으로 초기화하면 어떻게 될까요?
그렇게 되면 Layer 2의 각 unit의 g(z)값은 모두 같을 것이고, 세 unit은 똑같은 값으로 반복적으로 갱신될 것입니다.
따라서 우린 symmetry breaking 즉 θ을 $-ε≤0 ≤+ε$ 사이의 Random값으로 초기화하여 이를 해결합니다.
2. Forward Propagation으로 모든 unit에 대한 H(x)값을 연산합니다.
3. Cost 함수 J를 연산하도록 구현
4. Back Propagation 적용하여 갱신을 위한 각 unit의 g(z)와 $\frac{d}{dθ}*J(θ)$을 알아냅니다.
5. Gradient checking 해주기
이는 Gradient Descent Algorithm과는 다릅니다. 말 그대로 기울기 체크 즉 'Back Propagation'이 우리 의도대로 작동하는지 체크하는 것입니다.

우선 특정 지점 θ를 기준으로 하여 양옆으로 θ-ε과 θ+ε을 설정합니다. 이때 ε은 매우 작은 실수로 보통은 10^-4입니다.
이때 위식에서 말하는 $\frac{d}{dθ}*J(θ)$ 는 θ 지점에서 Back Propagation으로 구한 Cost의 미분값입니다. 그리고 $J(θ+ε)-J(θ-ε) \over 2ε$은 θ+ε와 θ-ε 두점의 기울기입니다. 이때 ε은 매우 작은 값이기 때문에, 한마디로 θ에서 Back Propagation으로 구한 Cost의 미분값과 실제 Cost 함수의 기울기값이 같은지를 비교하는 것입니다. 만약 다르다면 Back Propagation 알고리즘을 수정해야합니다.
위 방식은 θ가 실수일 때만 사용가능하고, θ가 vector라면 다음과 같은 방식을 사용해야 합니다.

θ가 n차원 vector일 때, vector내에 각 요소에 대해 편미분하여 Gradient checking를 해주면 됩니다.
6. Gradient Descent Algorithm이나 다른 advanced optimization algorithm을 이용하여 Neural Network 학습하기
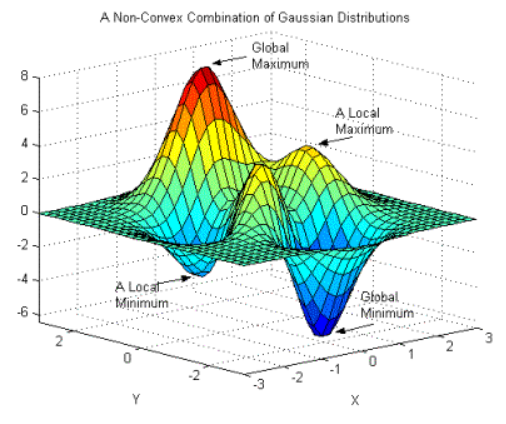
만약 Cost function이 non-convex해서 Local minimum으로 내려간다해도 꽤 괜찮은 local minimum으로 내려가기 때문에 크게 걱정할 필요가 없다.
요약
1) Input Unit 수 : 학습할 dataset의 features
2) Output Unit 수 : Class 종류의 수
3) Hidden Unit 수 : 보통은 Input Unit의 두배,
4) HIdden Layer가 많아질수록 성능은 좋아지지만 학습 속도가 느려진다.
5) Neural Network 학습 시 초기값 W* 을 어떻게 설정하느냐에 따라 도달하는 Local minimum이 달라진다.
'AI > Coursera ( Machine Learning )' 카테고리의 다른 글
| [머신러닝] 머신러닝 학습 시 고려해야 하는 것 : High Bias vs High Variance, Learning Curve (0) | 2020.05.03 |
|---|---|
| [머신러닝] 머신러닝 학습 시 고려해야할 것 : Test data와 Cv data란? (4) | 2020.05.03 |
| [머신러닝] Back Propagation(역전파) 정복하기 (2) | 2020.05.01 |
| [머신러닝] Neural Network를 이용한 XNOR 연산 그리고 Multi Classification (0) | 2020.05.01 |
| [머신러닝] 딥러닝의 시작 Neural Network 정복하기 1 (1) | 2020.04.30 |