시작하며
이번 포스팅에선 비용 함수(Cost Function)의 비용값을 최소화 하는 파라미터 θ를 찾는 경사 하강 알고리즘(Gradient Descent Algorithm) 에 대해 공부해보겠습니다.
경사 하강 알고리즘(Gradient Descent Algorithm)

경사 하강 알고리즘은 비용 함수 J(θ(0),θ(1))를 최소화 하는 θ를 구하는 알고리즘으로 머신러닝에서 굉장히 폭넓게 쓰입니다. 작동원리는 단순합니다.
- θ에 대해 임의의 초기값 즉 시작점을 잡습니다.
- 그리고 J가 최소가 될때까지 θ값 갱신을 반복하여 최솟값에 도달했을 때 해당하는 θ를 찾아냅니다.

- := : 대입 연산자
- θ 값을 갱신한다는 의미입니다.
- 'α 뒤에 곱해져있는 것'은 비용 함수 J의 미분값 입니다.
- α : learning rate
- 갱신되는 θ 값의 속도 를 결정합니다. 아무리 미분값이 크더라도 α가 작다면 갱신되는 속도가 느려지는겁니다.

이런 식으로 초기값 설정 후 반복적인 갱신을 통해 최종적인 minimum에 도달하는 것 이 최종 목표가 됩니다.
이제 알고리즘의 각 구성요소가 어떤 역할을 하고 어떤 특성을 가지고 있는지 좀 더 구체적으로 알아보겠습니다.
1) 미분 값(Derivative Term)

미분 값은 곧 해당 지점에서의 기울기 를 의미합니다.
만약 α가 일반적인 양수값이라면 θ(=w)가 반복적으로 갱신되면서 최종적으로 최솟값에 도달하게 될 것입니다.
θ의 갱신은 기울기 하강과 기울기 상승 두가지로 나뉩니다.

포물선의 대칭축을 기준으로 오른쪽 영역 에서 한 지점을 초기값으로 설정했다고 가정해보겠습니다.
이 경우 오른쪽 영역의 기울기 즉 미분값은 양수 일 것입니다. 그렇기 때문에 갱신 시 θ는 감소 하여 최솟값 지점으로 가깝게 이동하게 됩니다.

이번엔 포물선의 대칭축을 기준으로 왼쪽 영역 에서 한 지점을 초기값으로 설정했다고 가정해보겠습니다.
이 경우 왼쪽 영역의 기울기 즉 미분값은 음수 일 것입니다. 그렇기 때문에 갱신 시 θ는 증가 하여 최솟값 지점으로 가깝게 이동하게 됩니다.
이러한 이유로 경사 하강 알고리즘에선 초기값을 어디로 잡아도 결국은 최솟값으로 돌아가는 것입니다.
2) Learning Rate(학습 속도)
이번엔 Learning Rate가 지나치게 작을때와 클 때 를 비교해보며 이것이 어떤 의미를 갖는지 알아보겠습니다.

만약 Learning Rate가 지나치게 작다면 최솟값에 도달하기 위해 굉장히 많은 연산이 요구됩니다.
반대로 Learning Rate가 지나치게 크다면 θ가 반대쪽을 오가며 매우 큰 거리를 이동하게 되어 최솟값에서 점점 멀어지게 됩니다.
그렇기 때문에 적절한 Learning Rate를 설정하는 것은 매우 중요합니다.
Learning Rate는 속도에만 영향을 주는 것이 아닙니다.
만약 Learning Rate없이 미분값으로만 갱신을 진행하게 되면 최솟값으로 도달하지 않고, 제자리에서 진동할 수도 있기 때문에 Learning Rate를 곱하여 갱신값에 변화를 주며 최솟값에 도달하게 해야합니다.
3) θ의 수렴 조건

그렇다면 경사 하강 알고리즘은 어떤 조건에서 갱신을 멈추게 될까요?
함수는 극점에서의 기울기가 0 이라는 사실을 우리는 미적분에서 배웠습니다. 즉 만약 우리가 최솟값에 도달했다면 해당 지점에서 미분값이 0일 것이고 이 경우 바로 직전의 값과 갱신값 사이의 변화가 없을 것입니다.
이 경우가 Cost Function이 최소가 되는 경우이므로 멈추면 됩니다.
선형 회귀를 위한 경사 하강 알고리즘(Gradient Descent for Linear Regression)

이제 최적의 가설함수를 구하기 위해 경사 하강 알고리즘을 어떻게 적용하는지 알아보겠습니다.
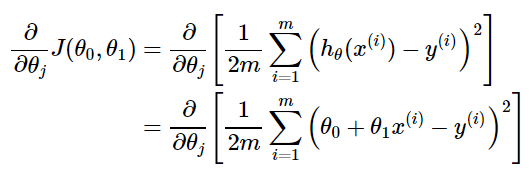

우선 비용함수 J 부분에 우리가 알고 있는 Cost Function 식을 대입해줍니다.

경사 하강 알고리즘에 적용한 결과입니다.
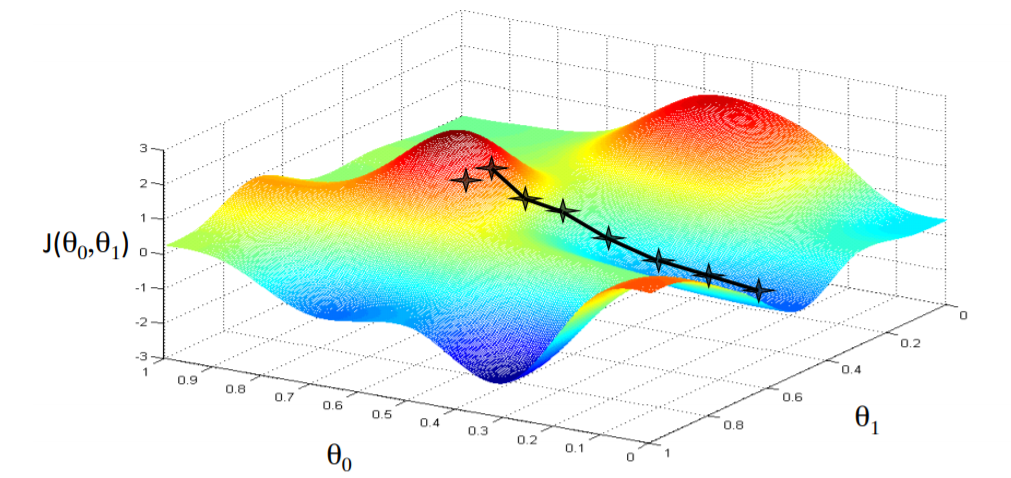
일반적인 등고선 그래프의 경우 전역 최솟값(Global minimum) 과 지역 최솟값(Local Minimum) 이 둘 다 존재합니다.
여기서 전역 최솟값이란, 등고선 그래프 전체에서 가장 작은 값을, 지역 최솟값은 특정 지역 내의 상대적인 최솟값을 의미합니다.
따라서 초기값을 어떻게 설정하느냐에 따라 Global minimum이 아닌 Local Minimum에 빠지게 되어 최적의 θ를 찾지 못할 수도 있습니다.

그러나 선형 회귀(Linear Regression) 의 경우엔 위 그림처럼 Bowl-Shaped Function의 형태 만을 가지기 때문에 Global minimum밖에 존재하지 않습니다. 그러므로 Linear Regression으로 필연적으로 Global minimum으로 수렴합니다.
Batch Gradient Descent Algorithm
이번 포스팅에서 우리가 배운 경사 하강 알고리즘은 Batch Gradient Descent Alogirithm 에 해당합니다.
Batch는 Total training set 입니다. 즉 갱신을 하는 매 단계마다 전체 Training set을 활용하였기 때문에 이런 이름이 붙게 되었습니다.
이러한 알고리즘엔 어떤 장단점이 있는지 알아보겠습니다.
-
장점
- 전체 업데이트가 한번에 이뤄지므로 계산의 횟수가 적습니다.
- 전체 데이터에 대해 미분값을 계산하여 갱신하므로 안정적으로 수렴해갑니다.
-
단점
- 한번의 갱신에 전체 Training set이 사용되므로 학습이 오래 걸립니다.
- 갱신 직전까지 전체 Training set의 오차를 가지고 있어야 하므로 상대적으로 많은 메모리가 요구됩니다.
- Local minimum에 빠지면 나오기가 어렵습니다.
요약
1) Gradient descent algorithm은 비용함수(Cost Function)를 최소화하는 θ를 찾기 위한 알고리즘으로 기울기에 따라 θ를 반복적으로 갱신하면서 비용을 최소화시키는 θ에 도달한다.
2) Learning rate는 알고리즘의 학습 속도를 결정한다.
3) 경사 하강 알고리즘은 갱신 직전 값과 갱신 값이 같을 때 종료 된다.
'AI > Coursera ( Machine Learning )' 카테고리의 다른 글
| [머신러닝] 다변수 선형 회귀(Multivariable Linear Regression )이란 (1) | 2020.04.30 |
|---|---|
| [머신러닝] 머신러닝 공부 전 꼭 알아야 할 행렬(Matrix)과 벡터(Vector) (0) | 2020.04.30 |
| [머신러닝] 비용함수(Cost Function)란 (10) | 2020.04.30 |
| [머신러닝] 지도학습(Supervised) vs 비지도학습(Unsupervised) vs 강화학습(Reinforcement) (0) | 2020.04.30 |
| [머신러닝] 인공지능 vs 머신러닝 vs 딥러닝 (2) | 2020.04.30 |