시작하며
저번 포스팅에서는 경사 하강 알고리즘에 대해 공부했었습니다.
이번 포스팅에서는 다음 포스팅에서 배울 다변수 경사 하강 알고리즘을 공부하기 전 행렬(Matrix) 과 벡터(Vector) 에 대한 기초를 다져보도록 하겠습니다.
행렬(Matrix)
행렬 이란 직사각형 모양의 숫자의 배열입니다. 이때 여러 숫자들을 모아서 한번에 표현했다는 것에 주목해야합니다.
왜냐면 행렬은 다량의 데이터를 한번에 표현할 수 있는 좋은 수단 이기 때문입니다. 여기서 조심해야할 점은 우리가 아는 표(Graph)와 행렬(Matrix)의 차이 를 명확하게 알아야 합니다.
- 표 는 여러가지 데이터를 효과적으로 시각화하기 위함입니다.
- 행렬 은 다량의 데이터에 대한 계산을 편리하게 하기 위함입니다.
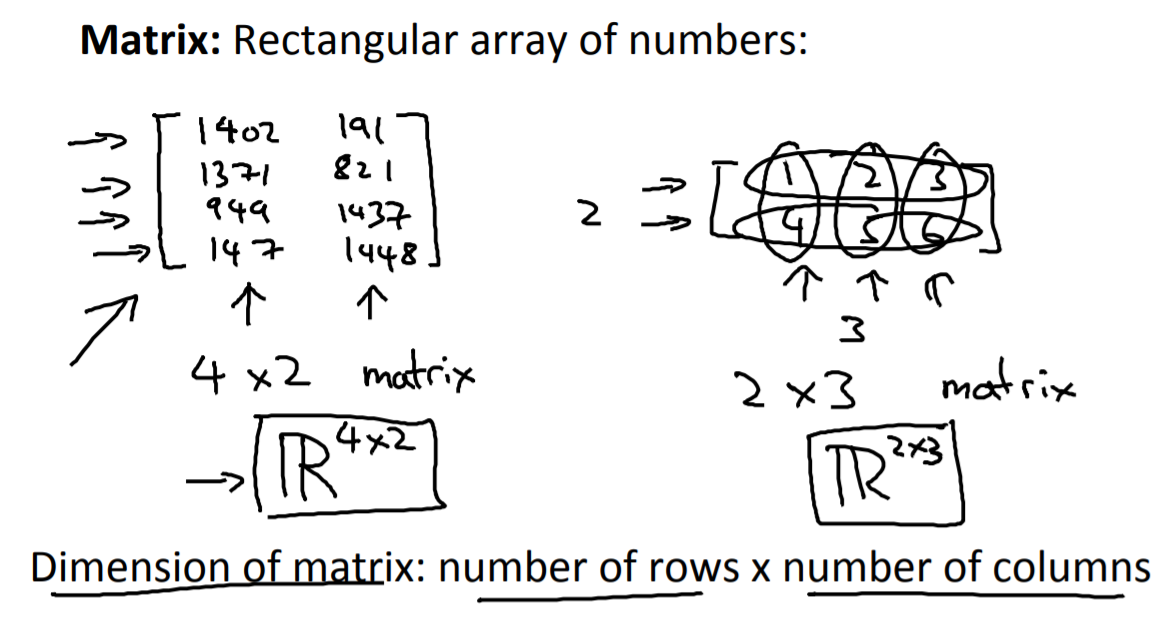
행렬의 차원(Dimension) 은 행(row) x 열(column)입니다. 위 이미지에서 이에 대한 두가지 예시를 들어주고 있습니다. (참고로 행은 가로줄, 열은 세로줄입니다.)

이번에 행렬의 요소 즉 내부에 들어있는 수에 대해 알아보겠습니다. 일반적으로 A라는 행렬이 있을 때 그 내부의 숫자를 지칭하는 방식 은 행렬의 이름 옆에 행과 열을 순서대로 기입하는 것입니다.
위 이미지를 예로 들자면 1402는 1행 1열에 있기 때문에 A(11)이 됩니다. (텍스트로는 표시가 어려워 이미지를 통해 표기법을 확인해주시면 감사하겠습니다.) 147의 경우에는 4행 1열에 있기 때문에 A(41)로 표기를 합니다.
벡터(Vector)

벡터(Vector)는 N x 1차원의 행렬(Matrix) 입니다. 즉 하나의 열을 가지며 여러 개의 행만을 가지기 때문에 벡터 내부 데이터의 수가 곧 벡터의 차원(Dimension) 이 됩니다. 따라서 벡터 y가 있을 때 이름 옆에 행만 기입해주면 됩니다.
기본적인 연산
이제 행렬과 벡터의 기본적인 연산에 대해 알아보겠습니다.

행렬의 덧셈 은 같은 위치에 있는 숫자끼리 더해주면 됩니다. 그렇기 때문에 같은 m x n 차원의 행렬끼리만 덧셈이 가능 합니다.

행렬에 단순한 스칼라 값(상수)을 곱하는 경우 입니다. 그냥 행렬의 각 숫자마다 해당 스칼라 값을 곱해주면 됩니다.

위에서 배운 두가지의 연산이 섞여있는 경우입니다. 이 경우 우리가 일반적으로 아는 사칙연산의 규칙과 동일하게 곱하기와 나눗셈을 먼저 진행해주고 나머지 합과 차 연산을 진행해주시면 됩니다.
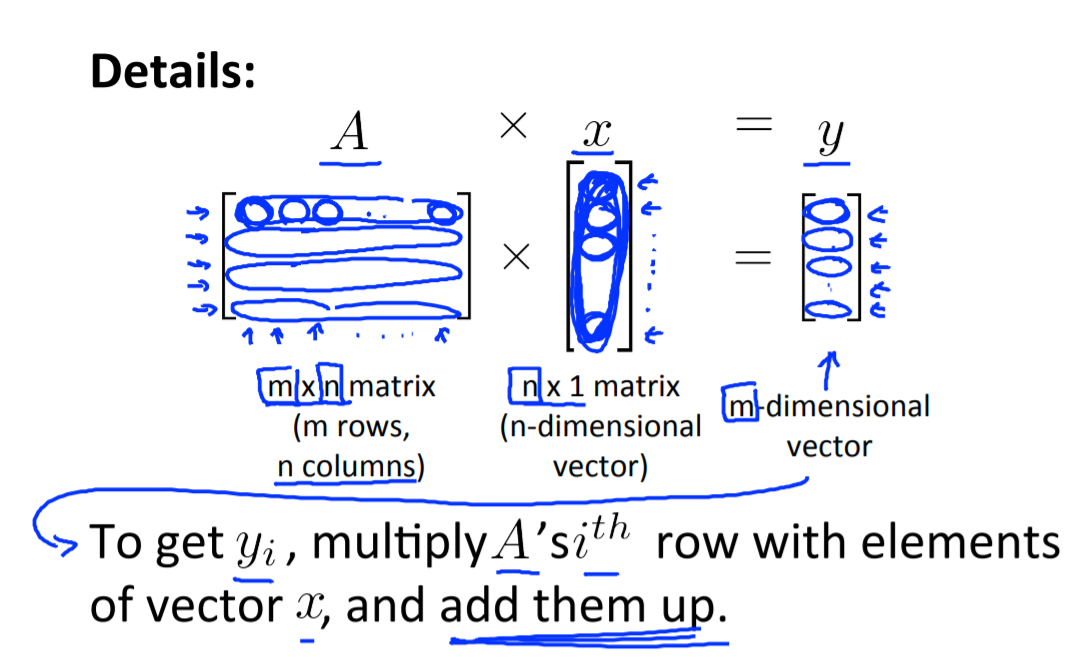
행렬과 벡터의 곱 입니다. M x N 차원의 행렬 A와 N차원 벡터를 곱하면 M차원 벡터가 도출됩니다. 이때 유의해야할 것은 행렬의 열(column) N과 벡터의 행 N의 크기 가 같아야 곱 연산이 가능하다는 것입니다. 다음 예시를 살펴보며 어떻게 연산이 진행되는지 알아보겠습니다.
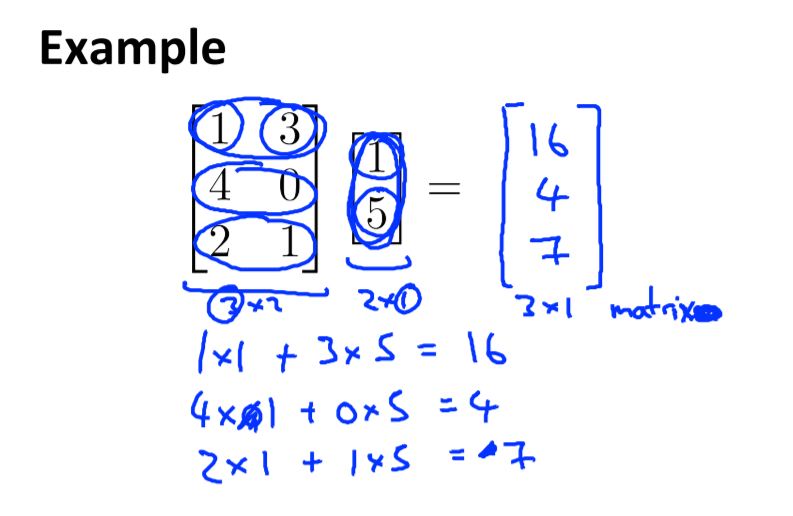
예를 들어 3 x 2 행렬과 2차원 벡터의 곱의 경우입니다. 쉽게 말씀드리며 행렬의 3개의 행([1,3],[4,0],[2,1])을 각각 떼어서 벡터와 같은 위치에 있는 숫자끼리 곱한 후 더한 Sum이 결과로 나오는 벡터의 데이터 하나가 됩니다.

또 다른 예시로 3 x 4 행렬과 4차원 벡터의 곱입니다.
행렬의 장점
머신러닝에서 행렬이 가지는 가장 큰 장점 중 하나는 복잡한 식도 행렬을 통해 간단하게 표기 할 수 있다는 점입니다.

우리가 자주 예시로 들던 Housing Price를 보겠습니다. 기존에 주어진 데이터에 대한 가설함수가 주어졌을 때 우린 데이터를 x에 대입하여 적절한 y값을 예측했었습니다.
하지만 다음과 같이 가설함수 h = X * a 형태로 Matrix를 이용하여 식을 변환하며 훨씬 간단하게 표현할 수 있습니다.
- X : Matrix / Housing Size값을 모아놓은 행렬
- a : Vector / 가설함수 h의 매개변수 θ를 모아놓은 벡터
왜 Matrix를 통해서 표현하려고 하는 것일까요? 원래는 Housing Price에 대한 가설함수 H(x)의 매개변수인 θ는 2개이기 때문에 Matrix가 아닌 대수적인 형태로도 계산이 가능합니다.
하지만 좀 더 정확한 Housing Price 예측을 위해 Size이외에 집의 층수 등 다양한 특징(feature)이 고려되어 매개변수 θ가 100개로 늘어난다면, 이러한 경우에는 대수적인 형태로 표현하기 어렵기 때문에 Matrix로 변환하여 표현하는 것이 필요할 것입니다.
행렬(Matrix) x 행렬(Matrix)
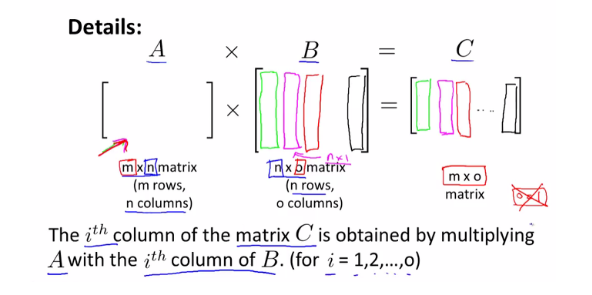
행렬(Matrix) x 행렬(Matrix)은 위에서 우리가 배웠던 행렬 x 벡터에서 벡터 대신 행렬 이 들어갔다고 생각하면 됩니다.
역시 마찬가지로 유의해야할 점은 한쪽 행렬의 열(column)과 다른 한쪽의 행(row)의 크기 가 같아야 한다는 점입니다.
계산 방식 은 위 이미지 기준으로 B 행렬의 o개의 열을 각각 하나씩 떼어서 벡터로 생각하고 전체 A 행렬과 n x 1 차원의 벡터의 곱을 한다라고 생각해주시면 이해하기 편합니다.

설명을 보충할 예시입니다.
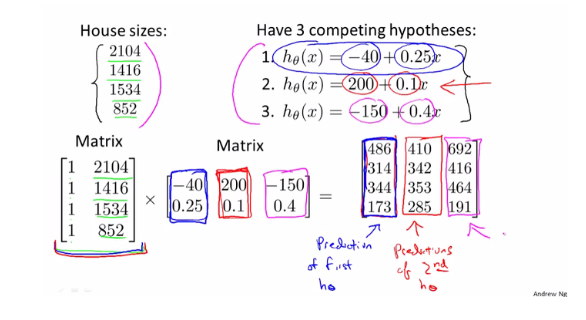
같은 Housing Price 예시이지만 이번에 가설함수가 세개 인 경우입니다. 이 경우에도 Matrix를 이용하면 간편하게 식을 세워 계산할 수 있습니다.
Matrix의 특성

1) Matrix x Matrix에선 교환 법칙이 성립하지 않습니다. 다만 Scalar x Matrix에선 교환 법칙이 성립합니다.

2) Matrix x Matrix에서 결합 법칙은 성립합니다. 즉 곱 연산에서 순서는 상관이 없습니다.
단위행렬(Identity Matrix)

왼쪽 위에서 오른쪽 아래 대각선 방향의 성분이 1이고 다른 성분은 모두 0인 n차 정사각행렬 을 n차 단위행렬(Identity Matrix)이라고 하고 'I' 로 기호화합니다.
이때 정사각행렬 은 행과 열의 크기가 같은 행렬을 의미합니다. 우리가 어떤 변수에 1을 곱한다고 해서 그 변수가 바뀌지 않듯이 어떤 M x N 행렬에 N x N 단위행렬 I를 곱한다고 해서 A 행렬이 바뀌지 않습니다. 그렇기 때문에 행렬 x 단위 행렬의 관계에선 교환법칙이 성립됩니다.
역행렬(Inverse Matrix)

대수적인 측면에서 역수가 있다면 행렬엔 역행렬이 있습니다. 우리가 일반적으로 3의 역수를 떠올릴때는 3과 곱해서 1을 만드는 수를 떠올립니다.
마찬가지로 어떤 A행렬의 역행렬 이라는 것은 A행렬과 곱하여 단위행렬을 만드는 행렬을 의미합니다. 이를 A^-1 로 기호화합니다.
행렬 x 역행렬의 관계에선 교환 법칙이 성립합니다. 특이행렬과 퇴화행렬은 역행렬을 갖지 않습니다.(특이 행렬(singular)과 퇴화 행렬(degenerate)은 크게 중요하지 않으므로 따로 설명드리지는 않겠습니다.)
전치행렬(Matrix Transpose)

전치행렬은 열과 행을 바꾼 행렬 입니다. 예를 들어 A(3,2)였다면 A(2,3)으로 바꾸고 모든 숫자에 이것을 적용시켜 최종적으로 M x N이었던 행렬을 N x M으로 바꾸는 것입니다.
이러한 전치행렬은 Matrix 곱 연산에서 두 개의 행렬의 크기를 맞추는데 사용 됩니다. 크기를 맞춘다는 것은 아까 말씀드렷듯 한쪽 행렬의 행과 다른 한쪽의 행렬의 열의 크기를 맞추는 것을 의미합니다.
요약
1) 행렬(Matrix) 이란 직사각형 모양의 숫자의 배열이며, 다량의 데이터에 대한 계산을 편리하게 하는 것이 목적이다.
2) 벡터(Vector) 는 N * 1 차원의 행렬이다.
3) Matrix A * Matrix B 곱의 필수 전제 조건은 A 행렬의 열과 B 행렬의 행이 일치하여야 한다.
4) Matrix간의 곱 연산에서 결합법칙은 성립하지만 교환 법칙은 성립하지 않는다.
5) 이번 포스팅에서 배운 행렬의 종류로는 일반적인 행렬 이외에 단위행렬, 역행렬, 전치행렬 이 있다.
'AI > Coursera ( Machine Learning )' 카테고리의 다른 글
| [머신러닝] 데이터 전처리(Feature Scaling)을 이용한 경사 하강 알고리즘(Gradient Descent Algorithm) (1) | 2020.04.30 |
|---|---|
| [머신러닝] 다변수 선형 회귀(Multivariable Linear Regression )이란 (1) | 2020.04.30 |
| [머신러닝] 경사 하강 알고리즘(Gradient Descent Algorithm)이란 (5) | 2020.04.30 |
| [머신러닝] 비용함수(Cost Function)란 (10) | 2020.04.30 |
| [머신러닝] 지도학습(Supervised) vs 비지도학습(Unsupervised) vs 강화학습(Reinforcement) (0) | 2020.04.30 |