아무리 어려워도 한번 시작한 일은 끝까지 해라
- 안드레아 정 (에어본 회장) -
저번 포스팅에서 우리는 RNN을 이용하여 주어진 Time-Series 데이터를 이용하여 미래를 예측하는 forecasting에 대해 공부해보았습니다. 하지만 이전에 우리가 다뤘던 데이터들의 길이는 상대적으로 짧은 축에 속했습니다.
몇달이 아닌 몇 년 치의 데이터에도 RNN은 좋은 성능을 보일까요?
긴 시퀀스(상대적으로 많은 타임 스텝을 가지는 Time-Series Data)로 훈련하려면 많은 타임 스텝에 걸쳐 실행해야 하므로 RNN은 그만큼 매우 깊은 네트워크가 됩니다. 보통 이렇게 깊어진 RNN은 다음과 같은 문제가 발생할 수 있습니다.
- 깊어진만큼 Gradient Vanishing 문제나 Exploding 문제가 발생할 수 있습니다.
- 길어진 데이터를 처리하면서 Input data의 초기 타임 스텝을 점점 잊어버릴 것입니다.
이번 포스팅에서는 RNN으로 긴 시퀀스 데이터를 다루기 위해서 어떤 점을 보완해야하는지 알아보겠습니다. 그리고 더 나아가서 LSTM과 GRU까지 모든 것을 파헤쳐보겠습니다.
이번 포스팅은 RNN을 공부하고 정독하시면 더욱 효과적입니다.
[AI/Hands-On Machine Learning 2판] - [ 머신러닝 순한 맛 ] 시계열 데이터의 모든 것, RNN 정복하기!
[ 머신러닝 순한 맛 ] 시계열 데이터의 모든 것, RNN 정복하기!
사는 데 더 나은 방법을 찾아라 - 엘빈 토플러 - 코로나로 인해 가장 크게 떠오른 분야가 무엇이냐고 한다면, 저는 주식만한게 없다고 생각합니다. 우린 결국 돈을 벌고 싶고, 미래를 예측하여
box-world.tistory.com
RNN으로 긴 시퀀스 다루기
앞서 간단하게 언급한대로, Gradient Vanishing/Exploding 문제때문에 있는 그대로의 RNN을 바로 긴 시퀀스에 적용하는 것은 어렵다는 것을 알았습니다.
이전에 우리가 공부한 Neural Network에서도 깊을 경우 이러한 Gradient 문제가 존재했고, 이를 위해 Gradient Initialization / Fast Optimization / DropOut 등 다양한 해결 방법이 있었습니다.
이러한 방법은 RNN에도 똑같이 적용될 수 있는데, 딱 하나 Relu(수렴되지 않는 activation 함수)와 같은 방법은 도움이 되지 않고 되려 더 불안하게 만들 수 있습니다.
예를 들어 이유를 설명드리겠습니다. Gradient Descent 알고리즘에 의해 첫번째 타임 스텝에서 Output을 조금 증가시키는 방향으로 Gradient Update가 이뤄졌다고 가정해보겠습니다. 그런데 이러한 방향의 Update가 두번째에도, 세 번째에도 계속 반복된다면 Gradient Exploding 문제가 일어나게 됩니다.
즉 RNN에서는 Relu와 같은 함수가 Gradient 문제를 해결하는데 도움이 되지 않습니다. 작은 Learning Rate를 사용하면 이런 위험을 감소시킬 수 있지만, 간단하게 tanh 함수와 같이 '수렴하는' activation 함수를 사용할 수 있습니다.
Batch Normalization은 RNN에서 그다지 효율적이지 않습니다. 정확하게 말하자면 타임 스텝을 넘어갈 때 사용할 수는 없고 하나의 타임 스텝을 처리하는 Layer들 사이에만 적용할 수 있습니다. 그렇지만 크게 기대할만큼 좋은 성능을 내지 못합니다.
그럼 RNN에 잘 맞는 Normalization은 뭘까요? 그것은 바로 층 정규화(Layer Normalization)입니다. 2016년에 소개된 이 개념은 Batch Normalization와 비슷하지만, Batch 차원이 아닌 Feature 차원에 대해 정규화가 이뤄집니다.

말로만 하면 잘 감이 안오실텐데 위 그림을 보면서 다시 생각해보겠습니다. feature 1, 2로 이루어진 50개의 데이터가 있다고 했을 때, 기존 BN(Batch Normalization)은 50개의 데이터를 Batch라는 단위로 몇개 그룹으로 분할하여 각 그룹의 평균과 분산을 구하여 정규화를 진행합니다.
반대로 LN(Layer Normalization)은 Batch 단위가 아니라, 50개 데이터에 존재하는 feature 1의 값을 모조리 모아 정규화를 진행하고, feature 2를 모아 모조리 정규화하는 방식입니다.
이렇게 전체 데이터를 feature를 기준으로 정규화를 하면, 내가 뽑는 batch에 따라 통계값이 달라지지 않고, 데이터에 독립적으로 필요한 통계값을 계산할 수 있기 때문에 Training과 Test에서 동일한 방식으로 작동하게 됩니다.
LN도 BN과 마찬가지로 Input마다 하나의 Scale과 Shift 파라미터를 학습합니다.
LSTM(Long, Short-Term Memory)
RNN을 거치면서 데이터의 길이가 길 수록 초기 타임 스텝의 정보는 사라지게 됩니다. 이는 중요한 문제이고 이를 해결하기 위해 소실되지 않게 장기적인 메모리를 가진 여러 종류의 셀이 연구되었습니다. 이 중 현재 가장 많이 쓰이는게 LSTM입니다.
LSTM은 훈련이 빠르게 수렴하고 데이터 내 장기간의 dependancy를 감지할 수 있습니다. 코드 상에선 기존에 사용하던 SimpleRNN 대신 LSTM을 사용해주면 되겠습니다.
model = keras.models.Sequential([
keras.layers.LSTM(20, return_sequences=True, input_shape=[None, 1]),
keras.layers.LSTM(20, return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(10))
])
그렇다면 LSTM은 어떻게 작동할까요? 다음은 LSTM의 구조입니다.

셀 내부를 들여다보지 않는다면, LSTM 셀은 기존 한개의 셀에서 두개의 셀 $h_{(t)}$와 $c_{(t)}$을 받는다는 점 빼고는 정확히 일반 셀처럼 보입니다. 여기서 $h_{(t)}$는 단기 상태, $c_{(t)}$는 장기 상태를 의미합니다.
본격적으로 박스 내부를 하나하나 살펴보겠습니다. 핵심은 장기 상태 $c_{(t)}$에 저장할 것, 버릴 것, 그리고 읽어들일 것을 학습하는 것입니다.
장기 기억 $c_{(t-1)}$은 타임 스텝에 따라 네트워크를 지나면서 '삭제 게이트'를 지나 일부 기억을 잃고, 그 다음 덧셈 연산으로 '입력 게이트'에서 선택한 기억을 추가합니다. 그렇게 해서 만들어진 $c_{(t)}$는 별도의 변환없이 바로 출력으로 보내집니다.
$c_(t-1)$은 삭제 게이트를 지나 덧셈연산 후 복사되어(두 갈래로 나뉩니다) $tanh$ 함수로 전달되는데, 이는 '출력 게이트'에 의해 걸러집니다. 이것이 단기 상태 $h_{(t)}$입니다.(셀의 출력 $y_{(t)}$와 동일합니다.)
이제 현재 타임 스텝의 입력 벡터 $x_{(i)}$와 이전 단기 상태 $h_{(t-1)}$가 주입되는 네 개의 다른 FC Layer에 대해 사렾보겠습니다.
- 네 개 중 $g_{(i)}$를 출력하는 Layer는 input 벡터와 단기 상태를 분석하는 일반적이면서 Major한 Layer입니다. 기본 셀에서는 이 layer 외에 다른 것 없이 바로 $y_{(t)}$와 $h_{(t)}$를 출력했었습니다. 하지만 LSTM에서는 바로 출력되지 않고, 장기 상태에 가장 중요한 부분만 저장되고 나머지는 버립니다.
- 나머지 세 개의 layer는 Gate controller입니다. 이들은 logistic 함수를 사용하여 Output range가 0~1 사이입니다. 그림에서 보듯이 이들의 출력은 곱셉 연산으로 주입되어 0을 출력하면 게이트를 닫고, 1을 출력하며 게이트를 엽니다.
- 삭제 게이트 ($f_{(t)}$)는 장기 상태 $c_(t-1)$의 어느 부분이 삭제되어야하는지 제어합니다.
- 입력 게이트 ($i_{(t)}$)는 $g_{(t)}$의 어느 부분이 장기 상태 $c_{(t)}$에 더해져야 하는지 제어합니다.
- 출력 게이트 ($o_{(i)}$)는 장기 상태의 어느 부분을 읽어 현재 타임스텝의 $h_{(i)}$와 $y_{(i)}$로 출력해야 하는지 제어합니다.
꽤나 복잡해보이지만 간단하게 얘기하면 LSTM은 중요한 Input을 인식하고(입력게이트), 이 Input을 필요한 기간만큼 장기 상태에 저장하고(삭제게이트), 그리고 필요할때마다 이를 추출하기 위해 학습합니다.
다음은 하나의 샘플에 대해 타임 스텝마다 장기, 단기 상태와 게이트 출력값을 계산하는 법입니다.

핍홉 연결
일반적인 LSTM은 하나의 셀에서 입력 $x_{(t)}$와 이전 단기 상태 $h_{(t)}$를 받아들입니다.
그런데 게이트 제어기에 이 둘 외에도 '장기 상태'도 조금 노출 시키면 좀 더 많은 context(문맥)을 감지할 수 있지 않을까요?
그래서 제안된 것이 2000년대 핍홀 연결(peephole connection)이라 부르는 추가적인 연결이 있는 LSTM 변종입니다. 이것은 이전 장기 기억 상태 $c_{(t-1)}$이 삭제와 입력 게이트 $f_{(t)}$와 $i_{(t)}$에 입력으로 추가됩니다.
이는 성능을 향상하는 경우가 많지만, 매번 그렇지는 않기 때문에 직접 확인 후에 적용을 해야합니다.
GRU
GRU(Gated Recurrent Unit)은 2014년에 제안된 LSTM의 간소화된 버전입니다. 어떤 차이점이 있는지 살펴보겠습니다.

- 기존 LSTM의 장기 상태 $c_{(t)}$와 단기 상태 $h_{(t-1)}$가 $h_{(t-1)}$로 합쳐졌습니다.
- 하나의 게이트 제어기 $z_{(t)}$가 삭제와 입력 게이트 모두를 제어합니다. 이것이 1을 출력하면 삭제가 열리고 입력이 닫힙니다. 반대로 0을 출력하면 반대가 됩니다.
- 출력 게이트는 존재하지 않기 때문에 $h_{(t-1)}$가 매 타임 스텝마다 출력됩니다. 그러나 이전 상태의 어느 부분이 Major 층 ($g_{(t)}$)에 노출될지 제어하는 $r_{(t)}$가 있습니다.
다음은 계산 식입니다.

LSTM과 GRU는 RNN을 보편화하는데 매우 큰 역할들을 하였습니다. 그러나 100 타임 스텝 이상의 시퀀스에서 이들 역시 장기 패턴을 학습하는데 어려움이 있습니다. 이를 해결하기 위해 몇가지 방법들을 시도해볼 수 있습니다.
1D ConvolutionalLayer를 사용해 시퀀스 처리하기
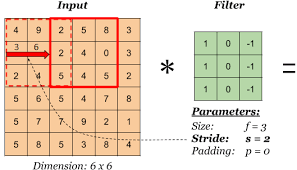
Convolutional Layer라고 하면 본래 CNN에서 이미지가 입력으로 들어왔을 때 이미지의 주요한 특징을 잡아내기 위해 3x3과 같은 필터(커널)을 이용해 슬라이딩하면서 2D feature feature map을 뽑아내는 과정에서 쓰이는 용어였습니다.
특히 일반적인 구조라면 이 Conv Layer를 거치면서 중요한 특성만 뽑아내기 때문에 점점 네트워크를 통과하면서 기존 이미지보다 사이즈가 작아집니다. 바로 여기서도 이러한 원리를 이용합니다.
일반적으로 Time-Series는 이미지처럼 사각형이 아니라 지렁이처럼 하나의 긴줄로 들어오기 때문에 1D에서 존재합니다. 결국 LSTM이나 GRU가 일정 타임 스텝 이상의 시퀀스를 다루기 어렵기 때문에 매우 긴 시퀀스가 들어왔을 때, 여기에 필터를 슬라이딩시켜 중요한 특징을 가진 1D feature map을 추출하여 데이터의 크기를 줄이자는게 핵심이 되겠습니다.
만약 10개의 필터를 사용하면 해당 layer의 출력은 10개의 1D 시퀀스로 구성됩니다. 이것을 10차원 시퀀스로 볼 수 있겠죠. 이 말은 즉 RNN의 Recurrent Layer(우리가 지금까지 RNN에서 보던 SimpleRNN Layer)와 1D Conv Layer 심지어 1D Pooling 층까지 섞어서 Neural Network를 구성할 수 있다는 뜻이 됩니다.
코드를 통해 구현을 살펴보겠습니다. stride = 1과 "same" 패딩으로 1D conv Layer를 사용하면 input과 output의 길이는 같습니다. 그러나 "valid" 패딩과 1보다 큰 스트라이드를 사용하면 output 시퀀스의 길이는 input보다 짧아지게 됩니다.
다음은 stride = 2를 사용해 입력 시퀀스를 두 배로 Down-Sampling(반으로 줄이는) 1D Conv Layer를 사용합니다. 이렇게 길이를 줄이면 GRU 층이 더 긴 패턴을 감지하는데 도움이 됩니다.
model = keras.models.Sequential([
keras.layers.Conv1D(filters=20, kernel_size=4, strides=2, padding="valid",
input_shape=[None, 1]),
keras.layers.GRU(20, return_sequences=True),
keras.layers.GRU(20, return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(10))
])
model.compile(loss="mse", optimizer="adam", metrics=[last_time_step_mse])
history = model.fit(X_train, Y_train[:, 3::2], epochs=20,
validation_data=(X_valid, Y_valid[:, 3::2]))
2) WAVENET
2016년도에 등장한 WAVENET은 앞서 살펴본 1D Conv Layer의 개념을 이용합니다. 이 네트워크는 Layer마다 팽창 비율(dilation rate)을 두 배로 늘리는 1D Conv Layer를 쌓습니다.
여기서 dilation rate를 설명하기 전 receptive field에 대해 상기해보자면, 하나의 뉴런이 받아들이는 이미지 내 local한 영역입니다. dilation rate는 계산량 증가 없이 이 receptive field를 효과적으로 높이기 위해 아래처럼 필터 내부에 zero padding을 추가해 강제로 receptive field를 늘립니다.

위 그림에서 파란색이 Input이고, 초록색이 feature map입니다. 여기서 Input의 진한 파랑 부분에만 weight가 있고, 나머지는 0으로 채워넣습니다.
이것이 등장한 이유는 필터의 크기를 크게하면 receptive field도 커져 이미지의 일반적인 feature를 잡기에 용이하지만 연산의 양이 늘어나고, Overfitting의 우려가 있습니다. 보통의 CNN에서는 이를 해결하기 위해 Pooling을 사용합니다.
그러나 Pooling을 사용하면 기존 정보의 손실이 일어납니다. 따라서 이러한 dilation rate를 활용한 dilated Conv는 pooling없이 receptive field의 크기를 크게 가져갈 수 있다는 점에서 이점을 가집니다.
그래서 결국 이 dilation rate가 커질 수록 filter의 크기가 커지면서 아래처럼 0으로 채워지는 부분이 많아집니다.

아래는 WAVENET의 구조인데, Input과 가까운 하위 층은 dilation rate가 적으므로, 필터의 크기가 작기 때문에 일반적인 것보단 단기 패턴을 학습하고, 점점 dilation rate가 높아지는 상위층으로 갈수록 일반적인 장기 패턴을 학습하게 됩니다. 이러한 원리로 dilation rate를 두 배씩 늘리는 형태의 네트워크로 아주 긴 시퀀스도 효율적으로 처리합니다.


다음은 WaveNet의 구현입니다.
model = keras.models.Sequential()
model.add(keras.layers.InputLayer(input_shape=[None, 1]))
for rate in (1, 2, 4, 8) * 2:
model.add(keras.layers.Conv1D(filters=20, kernel_size=2, padding="causal",
activation="relu", dilation_rate=rate))
model.add(keras.layers.Conv1D(filters=10, kernel_size=1))
model.compile(loss="mse", optimizer="adam", metrics=[last_time_step_mse])
history = model.fit(X_train, Y_train, epochs=20,
validation_data=(X_valid, Y_valid))
다음 포스팅에서는 RNN과 Attention 기법을 이용한 NLP에 대해 공부해보겠습니다. 오늘도 읽어주셔서 감사합니다. 행복한 하루 보내시길 바랍니다 :)
'AI > Hands-On Machine Learning 2판' 카테고리의 다른 글
| [ 머신러닝 순한 맛 ] 시계열 데이터의 모든 것, RNN 정복하기! (2) | 2021.07.28 |
|---|---|
| [ 머신러닝 순한맛 ] Regularization in 딥러닝의 모든 것 (2) | 2021.07.05 |
| [머신러닝 순한맛] 학습률 스케줄링의 모든 것 (1) | 2021.07.03 |
| [ 머신러닝 순한 맛] 전이학습은 어떻게 이뤄질까? with Code (1) | 2021.05.11 |
| [머신러닝 순한맛] 그레디언트 소실(Vanishing) / 폭주(Exploding)이란? (1) | 2021.05.02 |