사람들이 대개 기회를 놓치는 이유는 기회가
작업복 차림의 일꾼같아 일로 보이기 때문이다.
- 토마스 A. 에디슨 -
제 블로그의 'MIT 선형대수' 카테고리의 포스팅들은 Gilbert Strang 교수님의 Linear Algebra 강의를 기반으로 작성되었습니다. 이번 포스팅에서는 선형 대수 강의의 첫 포문을 여는 내용인만큼 기본적인 개념부터 시작하여 차근차근 나아가보려 합니다.
포스팅의 제목 그대로 문과생분들도 이해할 수 있을만큼 차분히 설명드릴테니 잘 따라와주셨으면 좋겠습니다:) (저 또한 고등학교때 문과생이었다가 컴퓨터공학과로 와서 수학 공부에 너무 힘들었기 때문입니다...^^;;;)
1. 선형 방정식 (Linear equation) 이란?
여기 두 개의 식이 있습니다.
$$\begin{cases}2x-y=0 \\ -x+2y=3\end{cases}$$
이것을 행렬로 표현하면 어떻게 될까요? 바로 위 식들의 계수들 (coefficients)만 가져와서 이들의 배열을 만들어주면 됩니다!
$$\begin{bmatrix}2 & -1 \\ -1 & 2 \end{bmatrix} \begin{bmatrix}0 \\ 3 \end{bmatrix} = \begin{bmatrix}0 \\ 3 \end{bmatrix}$$
이때 계수에 대한 행렬은 $A$, 미지수에 대한 벡터 (1차원 행렬은 벡터라고 칭합니다)는 $x$ 그리고 이들을 결합하여 만들어진 우변의 벡터는 $b$라고 합니다.
따라서 우린 이제부터 선형대수를 공부하는 것이므로 두개의 식을 보았을 때 고등학교에서 배운 연립 방정식이 아닌 저 식들을 행렬의 형태로 구성하여 '선형방정식' $Ax=b$의 형태로 문제를 접근해야합니다.
2. Row picture
앞서본 선형 방정식의 Row picture은 무엇인가요? 라고 누군가 물어본다면, 우린 저 선형방정식을 구성하는 두 식을 그림의 형태 즉 좌표평면상에서 표현해주면 됩니다! 다시 말해서 $2x-y=0$과 $-x+2y=3$을 좌표평면에 그려주면 되는것이죠.
아무래도 이것을 그리는 방법은 워낙 고등학교 때 많이 해왔던 일이기 때문에 아무 생각없이 그릴 수 있겠지만, 이것을 잘 생각해보면 결국 우린 한 직선이 지나는 두 점을 찾아 그것을 연결하고 있음을 떠올릴 수 있습니다.
$2x-y=0$는 $(0,0),(1,2)$와 같은 점들을 지나고, $-x+2y=3$은 원점을 지나진 않지만 $(-3,0),(-1,2)$와 같은 점들을 지난다는 것을 쉽게 떠올릴 수 있습니다. 이를 이용하여 그림을 그려보면 다음과 같겠죠!

여기서 우리가 보통 주목하는 부분은 각 직선의 $y$절편과 두 직선간의 교점 $(1,2)$ 같은 것들이 있습니다. 결국 우리는 선형방정식의 Row picture를 통해서 두 직선을 모두 만족하는 솔루션 $(1,2)$을 찾았다고 얘기할 수 있습니다.
3. Column picture (중요)
이제 우린 앞서 본 선형 방정식의 Column picture을 살펴보겠습니다. 이름 그대로 행렬의 Column (세로 줄)을 이용하여 다음과 같이 표현한 것이 Column picture라고 할 수 있습니다.
$$x\begin{bmatrix}2 \\ -1 \end{bmatrix}+y\begin{bmatrix}-1 \\ 2 \end{bmatrix}=\begin{bmatrix}0 \\ 3 \end{bmatrix}$$
이 방정식은 벡터 $\begin{bmatrix}2 \\ 1 \end{bmatrix}$와 $\begin{bmatrix}-1 \\ 2 \end{bmatrix}$를 $x$와 $y$를 통해 올바른 양으로 결합하여 $\begin{bmatrix}0 \\ 3 \end{bmatrix}$을 만들라고 우리에게 요구한다고 볼 수 있습니다. 즉 다시말해 우리에게 올바른 선형 조합 (linear combination)을 요구하는 것입니다!
이제 위 Column picture를 그림으로 표현하여 Column들을 결합해보겠습니다. 그림은 다음과 같습니다.
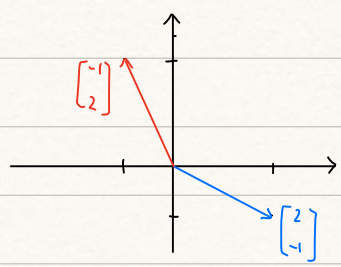
우리는 앞서서 $x=1, y=2$일 때 우변의 벡터 $\begin{bmatrix}0 \\ 3 \end{bmatrix}$를 얻는다는 것을 확인했는데, 이것이 위 그림을 통해서 기하적으로는 어떻게 도출될까요?
우선 $\begin{bmatrix}2 \\ 1 \end{bmatrix}$은 $x=1$이므로 변화없이 그대로 멈춰있지만, $\begin{bmatrix}-1 \\ 2 \end{bmatrix}$의 경우 $y=2$이므로 2배가 되면서 이것을 $\begin{bmatrix}2 \\ 1 \end{bmatrix}$과 더해주면 하늘색 벡터 즉 $\begin{bmatrix}0 \\ 3 \end{bmatrix}$가 도출됩니다.

그렇다면 $\begin{bmatrix}0 \\ 3 \end{bmatrix}$과 상관없이, 어떠한 값이든 $x, y$에 들어갈 수 있게되면서 솔루션은 좌표평면의 모든 공간을 채우게 됩니다. 여기까지는 2개의 방정식과 2개의 미지수를 가지고 다룰 수 있는 개념이었습니다.
이제는 3개의 방정식과 3개의 미지수에 대해서 다뤄보겠습니다.
$$\begin{cases}2x-y+0z=0\\-x+2y-z=-1\\0x-3y+4z=4\end{cases}$$
제가 여러분들에게 위 연립 방정식을 선형대수의 관점에서 어떻게 풀수 있습니까?라고 물어보면 머릿속에서는 1) Row picture 2) Column picture 두가지가 생각나야 합니다. 우선 Row picture의 관점에서 생각하려면 계수 행렬 (Coefficient matrix)부터 표현해야겠죠.
$$A=\begin{bmatrix}2&-1&0\\-1&2&-1\\0&-3&4\end{bmatrix} \; b=\begin{bmatrix}0\\-1\\4\end{bmatrix}$$
우선 저 선형 방정식의 솔루션을 구하기 앞서서 각 식에 대한 솔루션부터 생각해보겠습니다. $-x+2y-z=-1$의 솔루션부터 생각하면 $\begin{bmatrix}0 \\ 0 \\ 1 \end{bmatrix}$같은 것이 솔루션이 될 것이고 모든 해를 구하면 다음과 같은 평면으로 나타날 수 있습니다.

그리고 $2x-y+0z=0$나 $0x-3y+4z=4$의 경우엔 계산해보면 아래와 같은 평면으로 나타날 것입니다.

제 미숙한 그림 실력으로 이해 하시기 어려우실 순 있으시겠지만(^^;;) 중요한건 저 세 평면들은 평행하지 않기에 하나의 점에서 만나게 되고 그것이 곧 선형 방정식의 솔루션이 되는 것입니다. 우리가 느낄 수 있는건 2차원까진 Row picture로도 풀만 했지만 차원이 높아질수록 Row picture로 풀기 어려워집니다. 따라서 우리는 Column picture를 더욱 선호하게 됩니다!
그렇다면 아래와 같이 Column picture로 접근해보겠습니다.
$$x\begin{bmatrix}2 \\ -1 \\ 0 \end{bmatrix}+y\begin{bmatrix}-1 \\ 2 \\ -3 \end{bmatrix}+z\begin{bmatrix}0 \\ -1 \\ 4 \end{bmatrix}=\begin{bmatrix}0 \\ -1 \\ 4 \end{bmatrix}$$
결국 우리는 저 세가지의 벡터를 조합하여 (Linear combination하여) $\begin{bmatrix}0 \\ -1 \\4 \end{bmatrix}$를 얻고 싶은 것입니다. 그렇다면 위 Column picture를 기하적으로 표현하여 접근해보겠습니다.

이제 솔루션을 생각해보자면 가장 쉬운 솔루션 중 하나는 Column 3가 $b$와 동일한 $\begin{bmatrix}0 \\ -1 \\4 \end{bmatrix}$이기 때문에 $(0,0,1)$입니다. 이 점이 결국 앞서 Row picture에서 봤던 세 개의 평면이 만나는 한 점인 것입니다.
4. Non-singular ( invertible ) matrix
앞서서 특정 $b$에 대해 선형 방정식의 솔루션을 구하는 과정에 대해 살펴보았습니다.
그렇다면 앞서 보았던 저 선형 방정식은 모든 3차원 벡터 $b$에 대해 솔루션을 가질까요? 라고 물어본다면 이 말은 곧 저 선형 방정식을 구성하는 Column들의 linear combination은 3차원 공간을 모두 채울 수 있나요?를 물어보는 것입니다.
앞서 우리가 계속 다뤘던 아래 컬럼에 대해서는 우린 'yes'라고 얘기할 수 있습니다. 이런 행렬을 우리는 'non-singular' 혹은 'invertible' 행렬이라고 부릅니다. 반대로 모든 $b$에 대한 솔루션이 존재하지 않고 일부의 $b$에서만 존재한다면 이는 'singular' 행렬입니다. 당연하겠지만 우린 non-singular를 좀더 선호해야겠죠.
정리하자면 우리는 오늘 하나의 선형 방정식을 푸는 두 가지의 접근 1) Row picture와 2) Column picture에 대해서 살펴보았고, Non-singular ( invertible ) matrix의 개념까지 살펴보았습니다. 한가지 유념하면 좋을 것은 $Ax=b$에서 각각의 row와 $x$를 곱하는 관점은 내적 (dot product)의 관점이다라고 보고, Column picture의 관점에서 $A$의 컬럼을 기준으로 해를 푼다면 컬럼들의 Linear combination의 관점이다라고 이해해주시면 좋습니다.
오늘도 긴 저의 포스팅을 읽어주셔서 감사합니다. 행복한 하루 보내세요! :)
다음 포스팅도 보러 바로 고고!
[이론/MIT 선형대수] - [문과도 이해하는 선형대수 for 딥러닝] 2. 행렬 소거 (Elimination with Matrices)
[문과도 이해하는 선형대수 for 딥러닝] 2. 행렬 소거 (Elimination with Matrices)
성공의 커다란 비결은 결코 지치지 않는 인간으로 인생을 살아가는 것이다. - 알버트 슈바이처 - 안녕하세요 저번 포스팅에서는 선형 대수 공부의 첫 단원으로써, 선형 방정식을 Row picture와 Column
box-world.tistory.com