늘 명심하라. 성공하겠다는 너 자신의 결심이
다른 어떤 것보다 중요하다는 것을.
- 아브라함 링컨 -
곱셈(multiplication)과 역행렬(inverse matrix)은 선형 대수학에서 가장 기본이 되는 연산 중 하나입니다. 곱셈은 행렬 간의 연산으로, 두 개의 행렬을 곱할 때 결과 행렬의 크기와 요소는 입력된 두 행렬의 크기와 요소에 의해 결정됩니다. 반면 역행렬은 주어진 행렬의 역원(inverse)을 찾는 연산입니다. 역행렬은 주어진 행렬과 곱했을 때 단위행렬(identity matrix)을 얻을 수 있는 유일한 행렬입니다. 이번 포스팅에서는 이러한 행렬의 곱셈과 역행렬에 대해 자세히 알아보고, 이를 계산하는 방법에 대해서도 살펴보겠습니다.
해당 포스팅은 이전 내용을 공부하고 보시면 더욱 이해하는데 많은 도움이 됩니다.
[이론/MIT 선형대수] - [문과도 이해하는 선형대수 for 딥러닝] 2. 행렬 소거 (Elimination with Matrices)
[문과도 이해하는 선형대수 for 딥러닝] 2. 행렬 소거 (Elimination with Matrices)
성공의 커다란 비결은 결코 지치지 않는 인간으로 인생을 살아가는 것이다. - 알버트 슈바이처 - 안녕하세요 저번 포스팅에서는 선형 대수 공부의 첫 단원으로써, 선형 방정식을 Row picture와 Column
box-world.tistory.com
1. Matrix multiplication
이제부터는 두 행렬 $A$와 $B$를 곱하는 네 가지 방법에 대해서 하나하나 살펴보겠습니다.
1) $C_ij=\sum(A_ik*B_kj)$
우선 위 수식을 이해하기 위해 아래 $C=AB$의 상황을 보며 이해하겠습니다. 두 행렬 $A$와 $B$를 곱한 결과 $C$에서 3번째 row와 4번째 Column에 위치한 $C_{ij}$는 $A$의 세번째 row와 $B$의 네번째 Column간의 내적 (dot product)로 구할 수 있습니다!
$$C_{34}= a_{31}b_{14}+a_{32}b_{24}+\dots=\displaystyle\sum^n_{k=1}a_{3k}b_{k4}$$
그렇다면 두 행렬 $A$와 $B$는 언제 곱해질 수 있을까요? 바로 $A$가 $m \times n$이라면, $B$의 row의 개수는 A의 Column의 개수와 동일한 $n$이어야 합니다. 그리고 $B$의 Column의 개수는 어떤 것이 되든 상관이 없기 때문에 여기서는 $p$라고 하겠습니다.
그렇다면 각자 차원이 정의된 두 행렬을 곱했을 때 $C$의 차원은 $A$의 row 개수와 $B$의 Column 개수를 곱한 $m \times p$가 되는 것입니다!
2) 행렬 $\times$ 벡터로 바라보기
우리는 앞서 <어떤 행렬 E $\times$ 벡터 = E 컬럼의 선형 결합 (Linear combination)>이라는 것을 배웠습니다. 우린 행렬 간의 곱셈을 얘기하고 있는데 벡터가 필요한 Linear combination 얘기를 왜 꺼낼까요? 바로 두 행렬 A$와 $B$의 곱을 다음과 같이 $A$와 $B$의 각 Column간의 Linear combination으로 바라볼 수 있기 때문입니다.
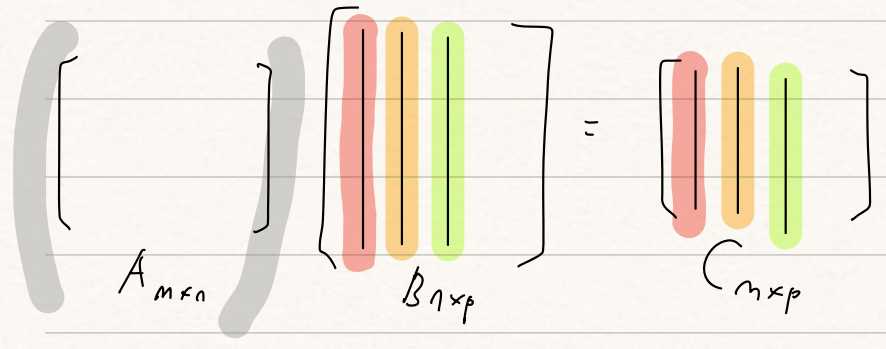
3) $A$의 한 row $\times$ $B$ = $C$의 한 row
앞서 Column의 관점에서 행렬의 곱셈을 바라봤다면, 이번엔 row의 관점에서도 바라볼 수 있겠죠! 2)에선 $A$의 전체와 $B$의 한 Column으로 $C$의 한 Column을 구했다면, row의 관점에서는 $A$의 한 row와 $B$의 전체를 곱하면, 다음과 같이$C$의 한 row를 구하는 것으로 이해할 수 있습니다!

예를 들어 $A$의 3번째 row를 기준으로 $B$의 첫번째 row와 내적하여 나온 값이 $C_{31}$, 두번째 row와 내적하여 나온 값이 $C_{32}$와 같이 되는 것이죠.
4) $A$의 한 Column과 $B$의 한 row의 곱셈으로 바라보기
이 방식은 바로 아래 예시와 함께 살펴보겠습니다!
$$\begin{bmatrix}2&7\\3&8\\4&9\end{bmatrix}\begin{bmatrix}1&6\\0&0\end{bmatrix}=\begin{bmatrix}2\\3\\4\end{bmatrix}\begin{bmatrix}1&6\end{bmatrix}+\begin{bmatrix}7\\8\\9\end{bmatrix}\begin{bmatrix}0&0\end{bmatrix}$$
말 그대로 같은 인덱스에 위치한 $A$의 Column과 $B$의 row를 곱하고, 그것들을 합쳐버리는 것입니다.
2. 역행렬 (Inverse matrix)
우리가 "이 행렬은 역행렬을 가질까?" 에 대해 얘기하려면 다음과 같은 몇가지 조건이 충족되는지를 보아야 합니다.
- 해당 행렬이 정사각행렬인가?
- invertible한가? or 해당 행렬은 non-singular 행렬인가?
그렇다면 우리가 해당 행렬이 invertible한지는 어떻게 알아야할까요? 다음 예시를 보며 알아보겠습니다.
$$A=\begin{bmatrix}1&3\\2&6\end{bmatrix}$$
제가 여러분에게 "행렬 $A$는 역행렬을 가질까요?"라고 물어보면 여러분들은 "A와 곱하여 단위 행렬 (identity matrix)가 나오게 하는 행렬이 있는지 찾아보겠습니다!"라고 대답하셔야 합니다.
그럼 우리는 단위 행렬은 행렬 $A$와 같은 차원인 $2\times2$를 가지는 $\begin{bmatrix}1&0\\0&1\end{bmatrix}$이라는 것을 배웠습니다.
그렇다면 앞서 배운 행렬 곱셈 방식에서 결과로 도출되야하는 단위 행렬의 '첫번째' Column $\begin{bmatrix}1&0\end{bmatrix}$는 행렬 $A$의 전체와 곱해질 행렬의 '첫번째' Column의 linear combination으로 도출된다고 배웠습니다. 그렇다면 그렇게 만들어주는 Column이 존재할까요?
안타깝게도 $A$ 행렬의 두 Columns $\begin{bmatrix}1&2\end{bmatrix}$와 \begin{bmatrix}3&6\end{bmatrix}은 직선 $y=2x$위에 있고, 해당 직선은 $\begin{bmatrix}1&0\end{bmatrix}$을 지나가지 않기 때문에 그러한 Column은 존재하지 않습니다. 이것이 우리가 역행렬의 존재유무를 판단하는 첫번째 방법입니다!
Singular matrix의 의미는 해당 행렬의 Linear combination으로 0을 만들 수 있다는 뜻입니다. 앞서 non-singular 행렬은 역행렬을 가지기 때문에 singular matrix는 역행렬을 가지지 못한다고 해석할 수 있습니다.
왜냐하면 어떤 combination으로 0이 도출된다면 역행렬을 곱했을 때 단위 행렬이 못나오고 0에서 못 빠져나온다는 뜻으로 해석되기 때문입니다!
앞서 본 행렬 $A$는 벡터 $\begin{bmatrix}3&-1\end{bmatrix}$를 곱했을때 0이 나옵니다. 그렇기 때문에 $A$는 singular matrix고 역행렬을 가질 수 없는 또 하나의 이유가 되는 것입니다.
3. 가우스-조던 소거법
가우스-조던 소거법은 선형 대수를 한번이라도 공부해보셨다면 익히 들어보았을 단어입니다. 쉽게 말해서 어떤 행렬 A에 대해 역행렬이 존재한다면, 그 역행렬을 구하는 방법입니다!
$$\begin{bmatrix}1&3\\2&7\end{bmatrix}\begin{bmatrix}a&b\\c&d\end{bmatrix}=\begin{bmatrix}1&0\\0&1\end{bmatrix}$$
위와 같이 행렬 $A$와 역행렬을 가진다면, 그 역행렬과 곱했을 때는 단위 행렬이 나와야할 것입니다. 그때 이 역행렬을 구해보세요!라고 얘기를 한다면, 다음과 같이 우선 그림을 그려주시면 됩니다!
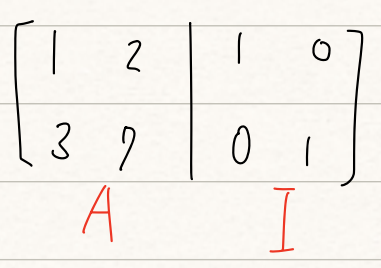
우리가 이전에 배웠던 소거법에 따라 행렬 $A$의 2번째 row에 '3'을 0으로 만들어주려고 합니다! 그러려면 첫번째 row에 3을 곱하여 2번째 row에 빼줘야할텐데요. 이때 $A$에만 3을 곱해서 빼주는것이 아니라, $I$에도 같은 연산을 똑같이 적용해주면 됩니다!

그러면 행렬 $A$는 상삼각행렬 (Upper triangle matrix)가 되는데요. 여기서 멈추는 것이 아니라, 행렬 $A$를 단위 행렬이 되게끔 윗쪽 방향으로 소거를 진행해주시는 겁니다!
그러니까 가우스-조던 소거법이라 하면 행렬 $A$와 $I$를 나란히 놓고 $A$를 단위 행렬로 바꾸는데 그때 적용되는 연산을 똑같이 $I$에 적용하여 나온 행렬이 $A$의 역행렬이 되는것입니다!
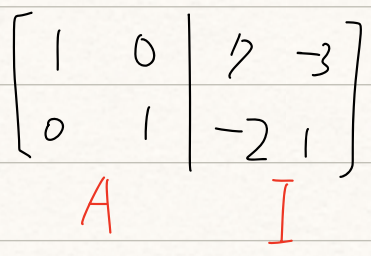
즉 위와같이 $A$의 두번째 row에 3을 곱해서 첫번째 row에 빼주면 나온 오른쪽 행렬이 역행렬이라고 할 수 있습니다!
긴 글 읽어주셔서 감사합니다! 행복한 하루 보내세요 :)
바로 다음 강좌로 고고!
[이론/MIT 선형대수] - [문과도 이해하는 선형대수 for 딥러닝] 4. 행렬 분해 (Matrix factorization)
[문과도 이해하는 선형대수 for 딥러닝] 4. 행렬 분해 (Matrix factorization)
의심으로 가득 찬 마음은 승리로의 여정에 집중할 수 없다. - 아서 골드 - 이번 포스팅에서 다룰 내용은 행렬 분해 (Matrix factorization)입니다. Matrix Factorization은 데이터를 분석하고 모델링하는데 널
box-world.tistory.com
'이론 > MIT 선형대수' 카테고리의 다른 글
| [문과도 이해하는 선형대수 for 딥러닝] 4. 행렬 분해 (Matrix factorization) (0) | 2023.03.13 |
|---|---|
| [문과도 이해하는 선형대수 for 딥러닝] 2. 행렬 소거 (Elimination with Matrices) (2) | 2023.03.08 |
| [문과도 이해하는 선형대수 for 딥러닝] 1. 선형 방정식 (The geometry of linear equations) (0) | 2023.03.01 |