″성공의 핵심 요소는 인내심이다.”
-Bill Gates-
시작하며
우리 저번 포스팅에서 Data Compression 또는 Dimentianality Reduction의 기본적인 원리를 알아보았습니다. 이번 시간에는 이러한 원리를 바탕으로 효과적으로 차원을 줄이는 알고리즘인 PCA(Principal Component Analysis) Algorithm에 대해 공부해보겠습니다.
한가지 유의할 점은 기존에 많은 분들이 PCA에 대해 다루실 때 수학적으로 접근하여 설명하는 부분이 저에게는 잘 와닿지 않았습니다. 그래서 저는 그보다는 쉽게 이해할 수 있도록, 빠지는 개념은 없지만 최대한 풀어서 설명하도록 하겠습니다.
이번 포스팅은 아래 포스팅을 공부하고 보시면 더욱 효과적입니다.
https://box-world.tistory.com/32
PCA Algorithm

여기 쥐와 유전에 대한 상관관계를 표현해놓은 Dataset이 있습니다. 2 개의 유전자는 Feature를 뜻하고, 6 마리의 쥐는 데이터를 의미합니다.

만약 Feature가 하나라면, 우리는 데이터를 위와 같이 하나의 직선 위에 나타낼 수 있습니다. 특히 이때 'Mouse' 1, 2, 3번의 값은 낮고 4, 5, 6번의 값은 높다는 것을 알 수 있습니다.

만약 Feature가 두개라면, 우리는 하나의 축을 추가하여 데이터를 다음과 같이 표현할 수 있습니다. 이때도 역시 비슷한 데이터들끼리 모여있다는 것(Cluster)을 확인할 수 있습니다.

만약 Feature가 세개라면, 다시 한번 축을 추가하여 데이터를 3차원 위에서 표현할 수 있습니다.

하지만 4개의 유전자라면 즉 Feature가 4개라면, 4차원이기 때문에 더 이상 데이터를 표현할 수 없습니다.

그래서 이제부터 우리는 PCA가 어떻게 4개 이상의 유전자를 측정할 수 있는지 알아볼 것입니다. 즉 4개 이상의 차원에 존재하는 데이터를 PCA를 이용하여 2차원으로 감소시켜 표현할 것입니다.
그리고 위 그래프에서 쥐 1,2,3과 4,5,6은 여전히 군집해있다는 것을 확인할 수 있습니다. 그래서 우리는 PCA가 어떻게 특정 Feature를 Data Clustering에 가장 중요한지 알려줄 수 있는지도 알아볼 것입니다.

우선 PCA가 무엇인지, 그리고 작동 원리가 무엇인지 알아보기 위해 다시 데이터의 Feature를 두개로 줄여보겠습니다.



그 다음 위 2개의 이미지처럼 Gene 1의 평균과 Gene 2의 평균을 도출하여 아래 이미지와 같이 데이터의 중심이 어디인지를 파악합니다.

그리고 데이터의 상대적인 분포는 변화시키지 않고 그대로 데이터의 중심을 원점으로 옮깁니다.


이제 원점을 지나는 랜덤한 직선을 하나 생성합니다. 그리고 데이터에 fit하도록 직선을 회전시키면 오른쪽 그림의 결과가 나옵니다. 그런데 데이터에 fit하다는 것은 어떤 의미이며, 어떤 방법으로 데이터에 fit한 직선을 구하는지

우리가 방금 랜덤하게 생성한 선에 데이터를 투영합니다. 그리고 이 선과 데이터의 거리를 측정하여 이 거리를 최소화하는 직선을 찾습니다. 즉 PCA에게 데이터에 fit한 직선이라는 것은 데이터들과 거리가 가장 작은 직선을 의미합니다.


이렇게 '데이터와 직선의 거리를 최소화한다는 것'은 원점에서 데이터가 투영된 점들까지의 거리를 최대화하는 선을 찾는다는 것을 의미합니다. 이 부분이 이해가 안될 수도 있는데 오른쪽 이미지처럼 데이터와 fit한 선을 찾았을 때 왼쪽의 이미지보다 원점에서 투영된 점들까지의 거리가 늘어나는 것을 볼 수 있습니다.
지금까지 우리는 데이터에 fit한 하나의 직선을 찾았습니다. 아직 긴가민가 하시겠지만 절 믿고 따라오시면 됩니다.


이제 보다 수학적으로 이해하기 위해 왼쪽 그림처럼 하나의 점만 생각해보겠습니다. 우선 데이터와 원점의 거리는 변하지 않습니다. 그리고 점을 직선에 투영할 때 직각을 이루게 됩니다.
이때 이를 오른쪽 그림처럼 직각삼각형으로 보면 점과 원점 사이의 거리 a는 변하지 않기 때문에 b와 c는 반비례 관계를 가지게 됩니다. 눈치가 빠르신 분이라면 PCA 입장에서는 점과 직선 사이의 거리를 줄이려고 하기 때문에 b를 줄이고 c를 늘리려할 것이라는 걸 알 수 있습니다. 다만 실제 구현에서는 b를 구해서 최소화 하는 것보단 원점에서 투영된 점의 거리인 c를 구해서 이를 최대화하려는 것이 훨씬 쉽습니다.


이를 이제 왼쪽 그림처럼 여러개의 점들에 확장하여 적용해보겠습니다. 우선 데이터들을 직선에 투영합니다. 그 다음 오른쪽 그림처럼 '6개의 점들' 각각과 '원점'과의 거리인 d1부터 d6까지 계산합니다. 그 다음 이들을 제곱하여 음수와 양수가 상쇄되는 것을 방지합니다. 그리고 이 값들을 모두 더하게 되면 그림 위쪽과 같은 식이 나오게 되고, 우리는 이를 거리 제곱의 합 'SS'라고 부릅니다.
즉 다시 말해서 제가 아까 말했던 원점과 데이터가 직선에 투영된 점 사이의 거리를 최대화하는 직선을 찾아야 한다는 것은 결국 SS 값을 최대화하는 직선을 찾아야 한다는 것과 같은 의미입니다.


이러한 과정을 거쳐 최대의 SS를 가지는 직선을 PC1이라고 지정합니다. 이 PC1은 0.25의 기울기를 가집니다. 이때 기울기가 0.25라는 말은 Gene 1이 4번의 단위만큼 증가할 때, Gene 2는 1번의 단위만큼 증가하는 것을 의미합니다. 이것은 대부분의 데이터가 Gene 1을 따라 분산되어 있고, 아주 적은 데이터가 Gene 2을 따라 분산되어 있다는 것을 의미합니다. 아마 이 문장이 잘 이해가 안가실텐데 다음 문단에서 이해가기 쉽게 설명해보겠습니다.

방금 설명을 '칵테일 레시피'라는 것으로 쉽게 비유해보겠습니다. Gene 1을 4 조각, Gene 2를 1조각 그리고 얼음을 넣고 섞었다고 생각해보겠습니다. 그러면 우리가 마실 칵테일에서는 Gene 1의 맛이 더 많이 느껴지겠죠? 이것이 분산되어있는 데이터에서 Gene 1이 더 중요하다는 의미와 일맥상 통하게 됩니다. 수학자들은 이러한 칵테일 레시피를 '선형 결합(Linear Combination)'이라고 부릅니다. 그리고 우리가 지금까지 본 이 PC1을 변수들의 선형 결합이라고 부르기도 하지만 저는 이런 어려운 용어를 쓰지 않겠습니다 :(
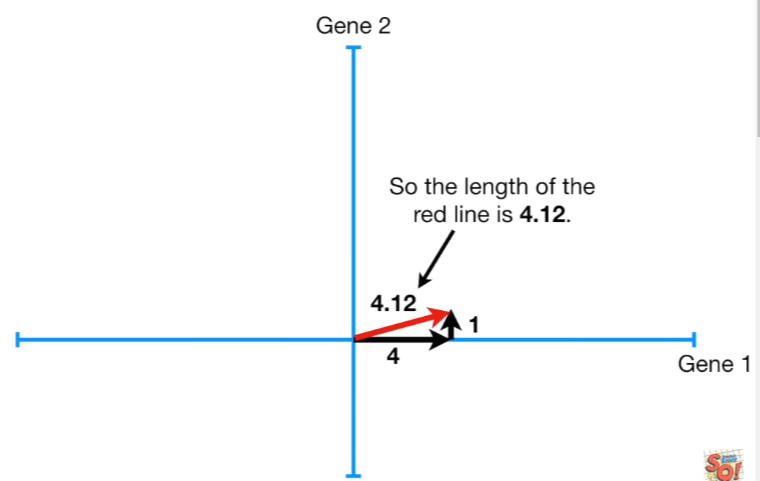
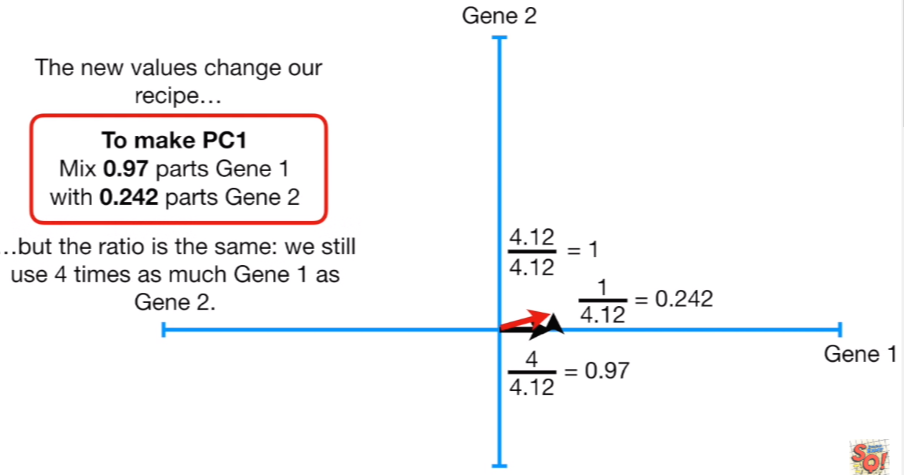
이어서 우린 피타고라스의 정리를 이용해서 빨간색 선의 길이를 계산할 수 있습니다. 12+42=17이므로 결과값은 √17=4.12가 됩니다. 그리고 SVD(특이값 분해)라는 것을 통해 우리가 도출한 가장 적합한 PC1의 단위벡터를 구해줄 것입니다. 이때 SVD 적용을 위해 빨간색 선의 길이는 1이 되어야 하기 때문에 세 변을 4.12로 모두 나누어줍니다. 하지만 레시피에 들어가는 value값만 바뀌었을 뿐 비율은 여전히 동일합니다.

다시 우리의 데이터로 돌아와보겠습니다. 현재 데이터와 방금 우리가 SVD를 통해 구한 PC1에 대한 단위벡터가 있습니다. 이때 이 단위 벡터를 Gene 1의 0.97만큼과 Gene 2의 0.242 만큼으로 구성되어 있는 Eigenvector(고유 벡터)라고 합니다. 그리고 이때 비율에 해당하는 0.97, 0.242는 적재 점수(Loading score)라고 합니다.

그리고 우리가 위에서 구했던 원점과 투영된 점들의 거리 SS를 PC1을 위한 Eigen value라고 합니다. 그리고 이것의 제곱근을 PC1을 위한 Singular value라고 합니다.
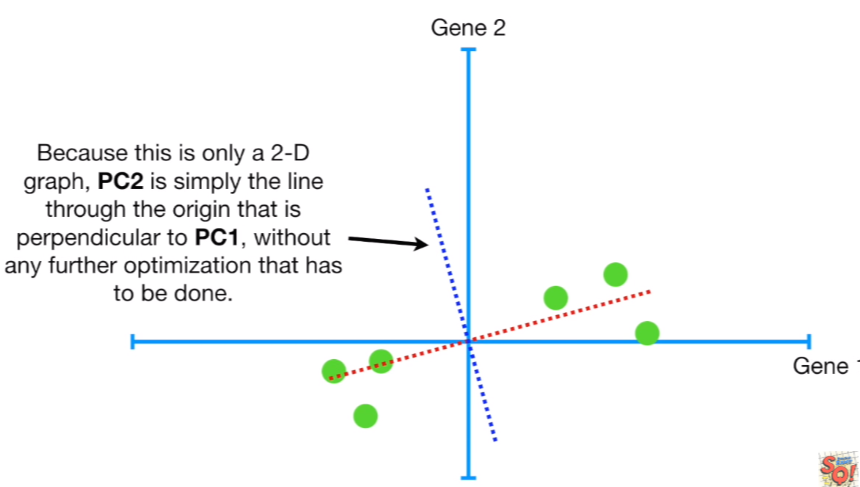

여기에 왼쪽 위 그림처럼 PC2라는 것을 하나 더 그려봅시다. PC2는 그냥 원점을 지나면서 PC1과 직교하게끔 그으면 되기 때문에 복잡한 최적화 작업을 거칠 필요가 없습니다.
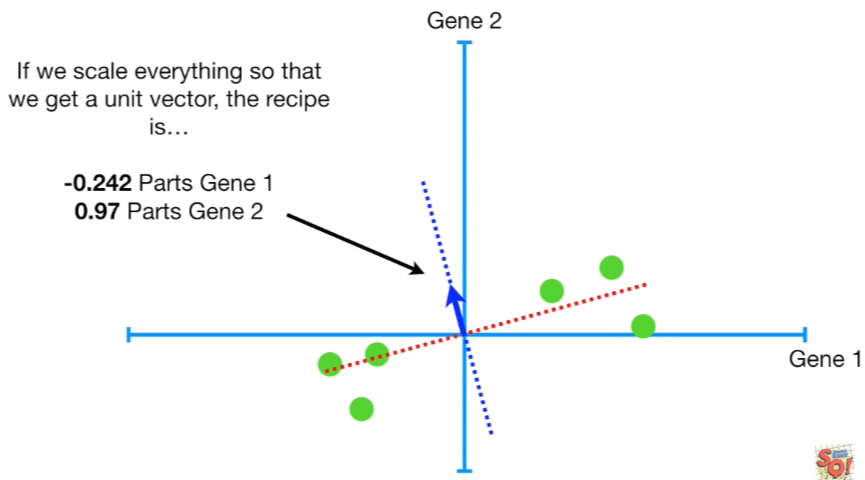
다시 말해서 PC2의 레시피는 직교하기 때문에 Gene 1의 -1 단위, 그리고 Gene 2의 4 단위가 될 것이며, 그리고 이를 이용해 PC2의 단위 벡터를 구하면 오른쪽과 같습니다. 그리고 우리가 PC1에 데이터를 투영했듯, PC2에도 데이터를 투영합니다.

최종적으로 구한 PC1과 PC2에 데이터를 투영한 결과입니다. 여기까지 읽는데 헷갈리시는 것도 많으실텐데 제가 마지막에 정리해드릴테니 따라와주시길 바랍니다! 이제 이제 마지막 단계를 위해 PC1을 수평으로 회전시킵니다.
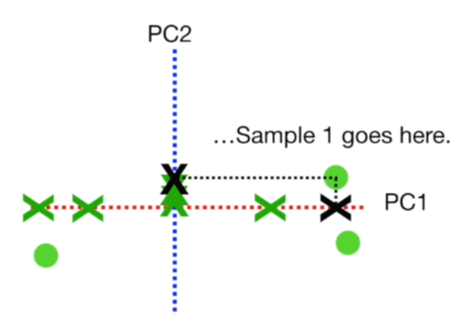
수평으로 회전시킨 후, 데이터가 어디있는지 찾기 위해 투영된 점들을 이용합니다. 예를 들어, Sample 1의 경우 위와 같이 연결하여 맵핑되는 것이고 최종 결과는 오른쪽과 같이 됩니다.
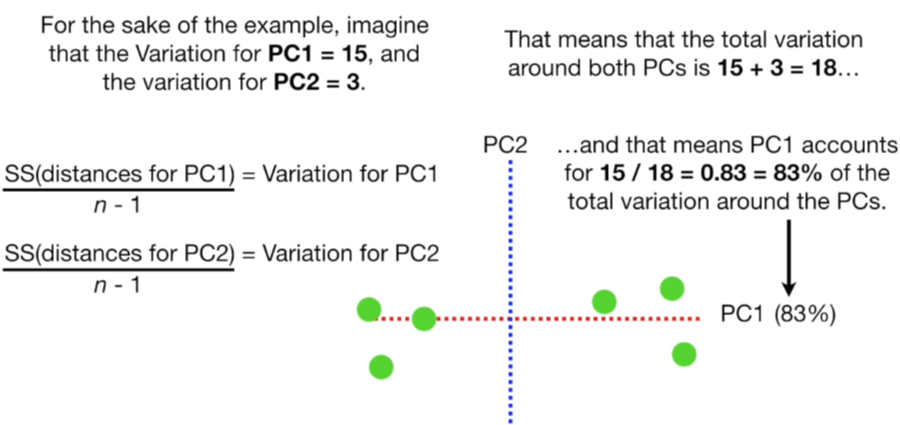
이제 마지막으로 한 가지 더 해야할 일이 있습니다. 우리가 이전에 PC의 Eigenvalue로 부르던 SS값을 왼쪽 그림처럼 샘플 사이즈 n -1으로 나눠 각각 PC1, PC2의 분산(Variation)을 구합니다.
예를 들어 PC1의 분산도가 15, PC2의 분산도가 3이라면, 전체 분산도는 18일 경우 이중 PC1이 차지하는 비율은 83%이고, PC2는 17%가 됩니다. 이 분산도가 높을 수록 데이터에서 차지하는 비중이 높다는 것을 의미합니다.
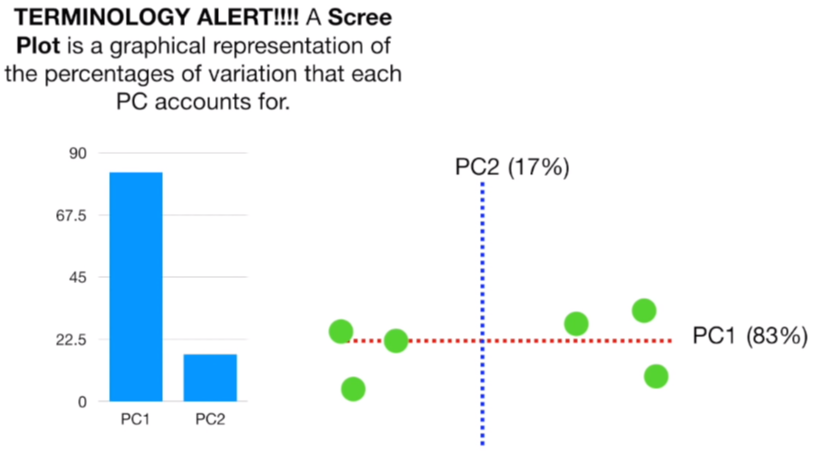
오른쪽은 이를 보기 쉽게 Scree plot이라는 것으로 나타낸 것입니다. 최종적으로 나온 이 결과 4개의 Feature를 가져 4차원으로 표현되던 데이터를 2차원으로 감소시킨 결과입니다.
요약
1) 데이터에 fit한 직선 PC1을 구합니다.
2) 기존에 데이터가 n차원이었다면, 원점을 지나며 기존 PC들과 직교하는 직선 n개를 생성합니다.
3) 각 PC의 분산도를 구하고 Scree plot을 이용하여 비교하기 쉽게 시각화합니다.
4) 내가 만약 줄이려는 차원이 m차원이라면 분산도가 높은 순으로 m개 만큼의 PC만 남기고 나머지는 걷어냅니다.
5) 이제 m개의 PC만 남았기 때문에 m차원이락 할 수 있고 여기에 데이터를 투영하면 끝입니다.

이제 좀더 복잡한 예시를 보겠습니다. 이번엔 Feature가 3개이고, 데이터는 오른쪽과 같이 3차원으로 표현됩니다. 우리는 이 데이터를 2차원으로 감소시킬 것입니다.

이제 데이터의 중심을 원점으로 옮긴 후 데이터가 가장 fit한 즉 SS값을 최대로 만드는 선을 찾아냅니다. 이 점선은 PC1을 위한 선입니다.

그리고 우리가 구한 빨간색 점선의 기울기에 칵테일 레시피를 적용하면 위와 수치가 나오게 됩니다.(설명을 위해 수치를 구하는 과정은 생략하였습니다). 이 경우 Gene 3가 PC1에서 가장 중요하다고 할 수 있습니다.

그리고 빨간색 직선과 직교하면 원점을 통과하는 PC2를 생성합니다. 이때 Gene 1의 수치가 가장 크므로 PC2에서 제일 중요하다고 할 수 있습니다.

또 다시 PC1과 PC2와 직교하면서 원점을 지나는 PC3를 생성합니다.

그리고 PC1, PC2, PC3의 Eigenvalue 즉 SS를 이용하여 각 PC가 차지하는 분산도의 비율을 위와 같이 결정할 수 있습니다.

우리는 3차원에서 2차원으로 감소시키므로 저 PC들 중에서 분산도의 비율이 높은 순으로 PC1, PC2만 남겨놓고 나머지는 다 걷어냅니다.
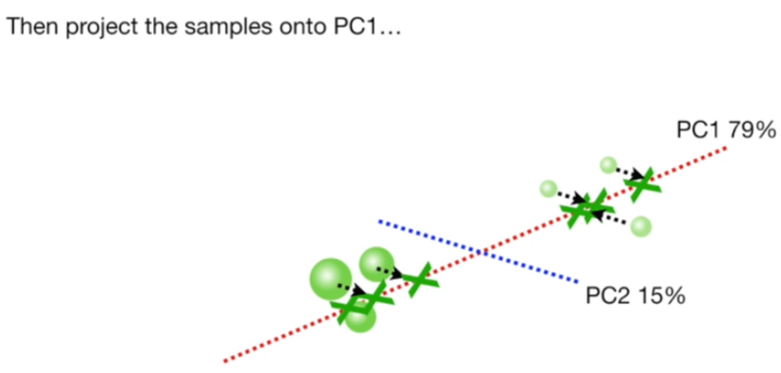
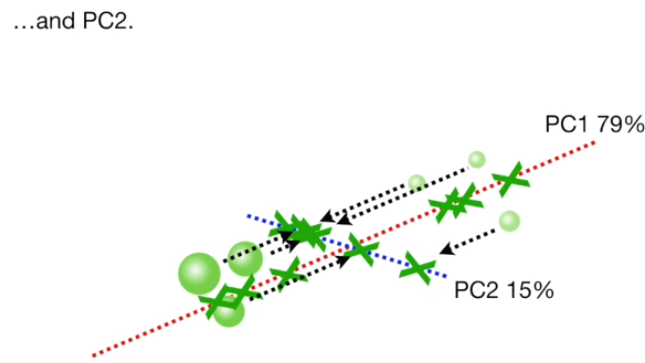
이제 데이터를 PC1에 한번, PC2에 한번 투영 시킵니다.

투영 시킨 후 보기 편하도록 PC1의 기울기를 0이 되게끔 회전시켜줍니다.
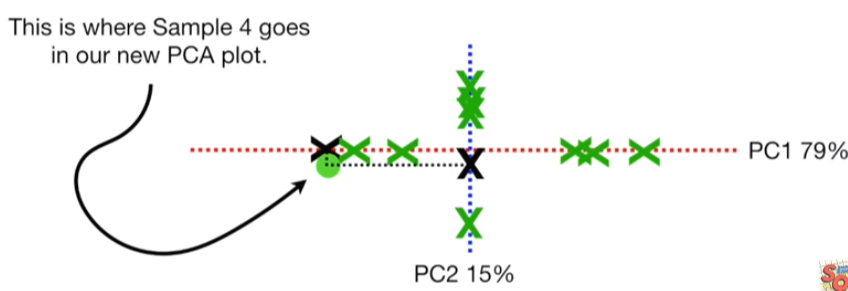
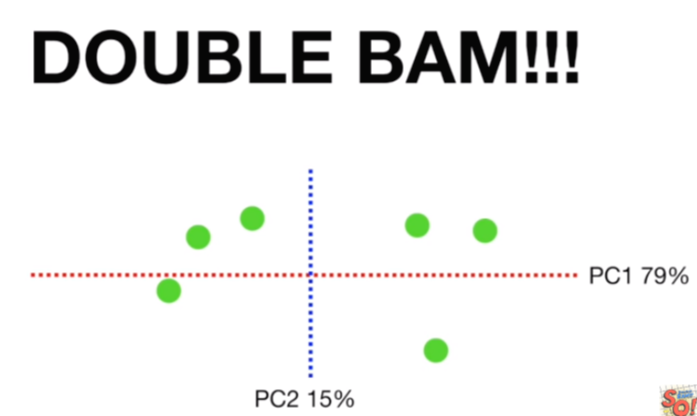
그리고 각 데이터가 PC1과 PC2에 투영했던 두개의 x를 이용하여 데이터를 다시 위치시키면 끝입니다.