"기술에는 품위와 친절이 녹아있어야 한다."
- 팀 쿡 -
시작하며
여기 암을 조기에 발견할 수 있는 인공지능을 만드는 개발자가 있습니다. 그 개발자는 우여곡절끝에 정확도 99.00%를 자랑하는 머신러닝 학습 모델을 만들어 냈습니다.
하지만 우리나라 기준으로 연간 암 발병률은 0.005%가 채 되지 않습니다. 열심히 만든 개발자에게는 99%도 겨우 만들어낸 훌륭한 모델이었으면 좋겠지만, 안타깝게도 이것으로 암을 조기에 발견하기에는 턱없이 부족한 정확도인것입니다.
이번 포스팅에서는 기존에 우리가 알던 분류(Classification)와는 다르게 100000개의 데이터 중에서 1개, 1000000000개 중에서 10개 꼴로 일어나는 것 같이 아주 극소수의 매우 작은 비율의 데이터 혹은 이상한(비정상적인) 데이터를 검출하는데 사용되는 이상 탐지(Anomaly Detection)에 대해서 공부해보겠습니다.
Anomaly Detection
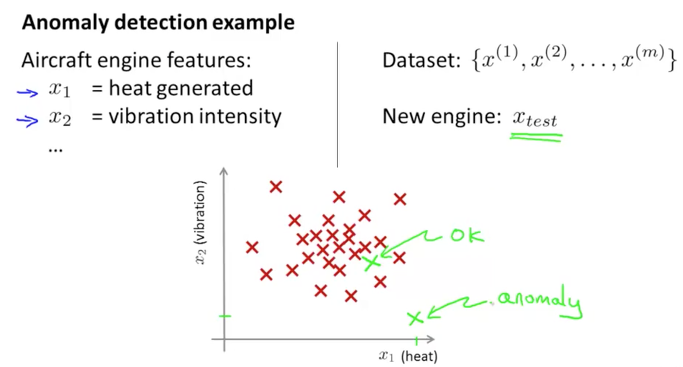
여기 비행기 엔진을 만드는 공장이 있습니다. 정상적인 엔진이라면 '열(heat)'이 높아질수록 '회전(vibration)' 또한 빨라져야 합니다. 이제 이것을 염두에 두고 데이터를 관찰해보겠습니다.
대부분의 데이터는 열과 회전의 비례관계를 만족하며 정상적인 엔진들이라고 판단되지만, 녹색으로 표시된 데이터는 이 비례관계를 만족하다고 하기엔 애매하다고 할 수 있습니다. 바로 이 녹색 데이터가 비정상적인 데이터 Anonmaly Data입니다.
이때 한가지 유의할 점은 'Anomaly Data Detection'이라는 것은 오류를 탐지하기 위한 알고리즘이 아니라, 전체 데이터 중 매우 작은 비율을 갖는 한쪽 데이터인 'skewed class'를 검출하는 알고리즘입니다.

그렇다면 m개의 dataset이 있을 때, $x_{test}$가 anomaly한 데이터인지 어떻게 판단할 수 있을가요? 여기에 바로 데이터의 밀도를 추정하는 함수(Density Estimation)인 $p(x)$가 이용됩니다. 이것의 함수값은 우리가 넣은 데이터 $x$가 정상적인 데이터일 가능성(probability)를 의미합니다. 그래서 이 함수값이 이따 살펴볼 특정 경계값 $(ε)$ 보다 작다면 Anomaly하다고 판단하게 됩니다.
우선 구체적으로 데이터의 밀도를 추정하는 함수 $p(x)$가 어떤 형태를 띄는지 알기 위해서는 몇가지 수학적인 개념이 필요한데 겁먹을 필요 없습니다! 저 또한 수학을 잘하지 못하기 때문에 제가 이해한대로 최대한 쉽게 설명해드릴테니 믿고 따라와주시면 됩니다. :)

우선 확률 밀도 함수(Probability Density Function)라는 개념부터 살펴보겠습니다. $x = a$일 때 함수값이 $f(a)$라는 것은 어떤 feature $x$가 $a$라는 값을 가질 상대적인 가능성을 의미합니다.
혹은 이 함수값은 밀도를 의미하는데 내가 input으로 넣은 데이터의 밀도가 크다는 것은 결국 나랑 비슷한 값을 갖는 데이터가 많다는 것이기 때문에 정상적인 데이터일 확률이 크다고 이해하셔도 됩니다.
즉 상대적인 가능성을 뜻하는 $f(a)$가 낮을수록 feature $x$에서 $a$라는 값이 적게 나타나는 것이기 때문에 Anomaly할 확률은 그와 반대로 커지게 됩니다.
이 확률 밀도 함수라는 개념을 기반으로 밀도를 추정하는 방법에는 'parametric'과 'non-parametric'이 있는데 이중 우리가 이용할 방법은 'non-parametric'입니다.

'parametric'은 우리가 사용할 dataset의 모든 feature가 '정규분포'를 따른다고 가정하고 밀도를 추정합니다. 즉 위 이미지처럼 종 모양의 형태를 띄는 정규분포는 feature $x$에 대해 평균에 가까울수록 밀도가 커지기 때문에, 평균과 비슷한 데이터가 제일 많을 것이라고 가정하고 밀도를 추정하는 것입니다.
그러나 우리가 일상 생활에서 발견하는 대부분의 데이터는 이런식의 예쁜 정규분포를 만족하지 않습니다. 따라서 순수하게 관측된 데이터만으로 확률밀도함수를 만드는 'non-parametic'을 이용하여 우리는 밀도를 추정할 것입니다.
머신러닝에서 사용하는 'non-parametic' 밀도 추정 방법 중 하나가 '커널 밀도 추정(Kernel Density Estimation)'입니다. 즉 커널이라는 것을 이용하여 확률 밀도 함수를 만들겠다는 것인데, 이것은
1) 전 구간에서 함수값이 양수여야 하며 $K(x) >= 0$
2) 대칭적이어야하고 $K(x) = K(-x)$
3) 함수의 중앙에서 멀어질수록 함수값이 감소해야합니다. $K'(x) <= 0 for every x >0$

이를 만족하는 커널에는 위와 같이 4종류가 있는데, 어떤 커널을 고르느냐는 중요한게 아니기 때문에 이중 계산이 간편한 '가우시안 커널(Gaussian Kernel)'을 사용하겠습니다.

우선 여기에 하나의 feature에 대한 dataset이 있습니다. 그리고 Kernel을 이용하여 특정 feature의 확률 밀도 함수인 'KDE(Kernel Density Estimation)'를 구하는 법 은 다음과 같습니다.


우선 각 데이터 $x_{(i)}$ 하나 당 $x_{(i)}$를 중심으로 하는 가우시안 커널을 하나씩 생성해줍니다. 그리고 더해주면 오른쪽 그림의 파란색 함수에 해당하는 KDE를 구할 수 있습니다.
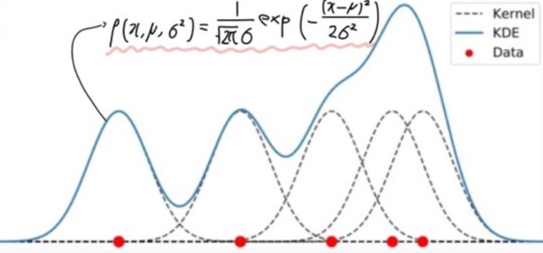
이해를 위해서 제가 단계를 나눠 KDE를 구하는 방식을 설명드렸지만, 각 feature의 $μ$(평균) 그리고 $σ$(표준편차)를 구하여 위 공식에 대입하면 별도의 단계없이 한번에 '해당 feature의 KDE'를 구할 수 있습니다.

여기서 중요한 것은 각 feature의 가우시안 커널 공식에서 h에 해당하는 'bandwidth'입니다. 이 bandwidth 가 너무 커지면 KDE가 완만해져서 Anomaly를 찾기 어려워지고, 반대로 너무 작아지면 KDE가 뾰족해져서 중심에서 조금만 멀어져도 Anomaly라고 판단하게 됩니다. 따라서 우리에게 중요한 것은 적절한 'bandwidth'를 찾는 것입니다.
이제 우리는 하나의 feature에 대해 'KDE' 즉 확률 밀도 함수를 구하는 법을 알게 되었습니다. 이제 이것을 Anomaly 데이터를 검출하는 알고리즘에 적용하기 위해서는 몇가지 단계를 거쳐야 합니다. 마지막에 총정리를 할테니 계속 따라와주세요!
우선 dataset에 각 feature마다 하나의 KDE를 모두 구해줍니다. 그 다음 각 feature에서 나온 KDE를 모두 곱해주면 이것이 바로 $p(x)$가 됩니다.
이제 우리에게는 데이터가 Anomaly한지 검출할 수 있는 함수 $p(x)$가 있습니다. 이제 우리가 해야할 일은 dataset을 보았을 때, Anomaly한 것으로 추정되는 데이터 $x_{(i)}$를 함수 $p(x)$에 집어넣으면 됩니다. 그리고 이렇게 해서 도출된 함수값 $p(x_{(i)})$가 양수이지만 매우 작은 $ε$보다 작다면 Anomaly하다고 판단하고, 크다면 정상적인 데이터라고 판단하게 됩니다.
요약
1) 모든 Feature에 대해서, 각 Feature의 데이터들을 중심으로 하는 가우시안 커널을 생성하고 이들을 모두 더하여, 각 Feature에 대한 확률 밀도 함수 KDE를 만들어 냅니다.
2) 각 feature의 KDE를 모두 곱하여 $p(x)$를 구합니다.
*3) * dataset에서 Anomaly하다고 생각되는 데이터를 추려낸 후, 이 데이터들을 $p(x)$의 input으로 넣어서 그 값이 $ε$을 기준으로 작은지 큰지에 따라 Anomaly 데이터 여부를 판단하면 됩니다.

마지막으로 예시를 보면서 개념을 복습해보겠습니다. 여기 $x1$, $x2$ 두개의 feature를 가지는 dataset이 있습니다. 따라서 각 feature마다 $μ$(평균) 그리고 $σ$(표준편차)를 구하여 공식에 대입하여 'KDE'를 구합니다.
보시다시피 feature $x2$의 $σ$가 더 작아서 분포가 뾰족한 것을 볼 수 있습니다. 이제 이 두개의 KDE를 곱하여 $p(x)$를 도출하고 우리가 테스트해보고 싶은 데이터를 이 함수의 input으로 넣어주면 됩니다. 이때 $ε = 0.02$라고 가정하겠습니다.
우선 $x^{{1}}_{test}$의 경우는 함수에 넣었을 때 0.0426으로 0.02인 $ε$보다 크기 때문에 정상적인 데이터라고 판단합니다. 하지만 $x^{{2}}_{test}$의 경우 0.0021로 $ε$보다 작기 때문에 Anomaly한 데이터라고 판단하게 되고 실제 그래프를 보더라도 Anomaly한 데이터일 확률이 매우 커보입니다.
https://box-world.tistory.com/24
[머신러닝] 머신러닝 시스템 디자인 하기 : Precision, Recall, F score
시작하며 머신러닝 시스템을 디자인하면서 적용해볼 수 있는 방법들은 다양하게 존재합니다. 이번 포스팅에서는 여러 방법들 중에 하나의 최선의 방법을 골라 적용할지 판단하는 체계적인 방��
box-world.tistory.com
제가 이전에 위 포스팅을 통해 Skewed Class, Precision, Recall, F1 score의 개념에 대해서 다룬적이 있습니다.
바로 이번 포스팅에서 배운 Anomaly Detection을 위한 알고리즘의 성능을 측정하는데 쓰이는 대표적인 지표가 바로 이 Precision, Recall, F1 score입니다. 따라서 이 포스팅을 완벽하게 공부하신 후 위 포스팅을 보신다면 큰 도움이 될거라고 생각합니다.